Subtracting Fractions on a Number Line
- Subtracting Fractions on a Number Line
- Steps to Subtracting Fractions on a Number Line
- Subtracting Fractions on a Number Line – Example 1
- Subtracting Fractions on a Number Line – Example 2
- Subtracting Fractions on a Number Line – Summary
- Frequently Asked Questions on Subtracting Fractions on a Number Line
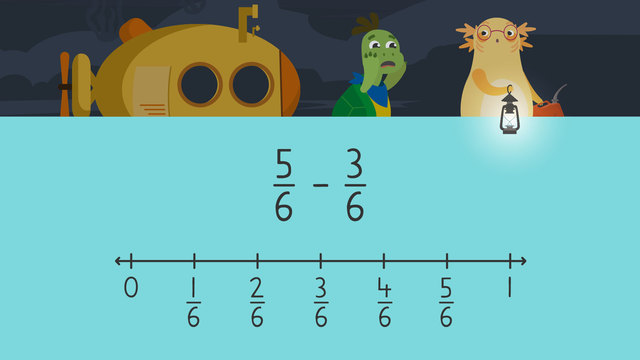

Basics on the topic Subtracting Fractions on a Number Line
Subtracting Fractions on a Number Line
When we learn about fractions and operations involving fractions we can use many different methods. In this learning text we are going to learn about subtracting fractions with common denominators. We will use one of the visual methods which is called a number line.
Steps to Subtracting Fractions on a Number Line
We know that a fraction has a top number (numerator) and a bottom number (denominator).
If you would like to know how to subtract fractions on a number line, please look at the steps below:
- Firstly, check if the fractions have common or like denominators.
- Secondly, divide the number line (between 0 and 1) into equal parts and label each part; the denominator is the indicator in how many parts the number will be divided between whole numbers.
- Then look at the first fraction and circle or highlight it on the number line.
- Finally jump from the highlighted fraction to the left as many times as shown by the numerator of the second fraction. Remember to simplify your answer if possible!
Subtracting Fractions on a Number Line – Example 1
Now that we know all of the steps for subtracting fractions on a number line we can look at the examples below and follow the process again. In our first example we are subtracting two fractions with a common denominator of six: $\frac{5}{6}$ minus $\frac{3}{6}$. In order to subtract two fractions using the number line, we divide the number line between zero and one into equal parts and label each part. Then we must find the first fraction on our number line and then jump to the left as many times as the numerator of the fraction we are subtracting shows. Our subtracted fraction has a numerator of three, so we must jump backwards three times. We have landed on $\frac{2}{6}$, so $\frac{5}{6}$ minus $\frac{3}{6}$ equals $\frac{2}{6}$.
Now we can simplify our answer. We can simplify $\frac{2}{6}$ to $\frac{1}{3}$ by dividing the numerator and denominator by a common factor which is two.
Subtracting Fractions on a Number Line – Example 2
Let’s look at how you show subtraction operations with fractions on a number line one more time.
This time we have been given $\frac{7}{8}$ minus $\frac{6}{8}$. Both fractions share the same denominator which is eight. We are going to repeat the same process as in the previous example.
- We divide the number line between zero and one into equal parts and label each part.
- Then we must find the first fraction on our number line and then jump to the left as many times as the numerator of the fraction we are subtracting shows.
- Our subtracted fraction has a numerator of six, so we must jump backwards six times.
- We have landed on $\frac{1}{8}$, so $\frac{7}{8}$ minus $\frac{6}{8}$ equals $\frac{1}{8}$.
- Now we can try to simplify our answer if possible. This time we cannot simplify further, so our answer is $\frac{1}{8}$.
Subtracting Fractions on a Number Line – Summary
In this learning text we learnt about subtracting fractions using a number line. Let’s look at the steps below for a quick review.
| Step # | What to do |
|---|---|
| 1. | Check that the fractions have the same, or common denominators. |
| 2. | Divide the number line into equal parts between 0 and 1 as shown by the denominators. |
| 3. | Find your first fraction on your number line and circle or highlight it. |
| 4. | Jump from the highlighted fraction to the left as many times as your second numerator from your second fraction indicates. |
| 5. | Simplify your answer if possible. |
To test your knowledge on subtracting fractions on a number line, have a look at our interactive practice problems, videos and worksheets.
Frequently Asked Questions on Subtracting Fractions on a Number Line
Transcript Subtracting Fractions on a Number Line
Axel and Tank are leaving the Oyster petrol station! "While I drive this thing, Tank, keep an eye on how much petrol we have left!" "You got it, partner! I'll track how much petrol we use!" Let's help keep track of the petrol left in the submarine by "Subtracting Fractions on a Number Line". We can use a number line like THIS to help us when subtracting fractions. To subtract fractions on a number line, first, check that the fractions have the same, or common, denominators. Five-sixths and three-sixths have the same denominator. Next, divide the number line into equal parts between whole numbers as shown by the DENOMINATOR. SIX is the denominator, so make six equal parts between whole numbers and label them like THIS. Now find five-sixths on the number line, which is HERE. Then, identify the numerator of the fraction we are subtracting, which is THREE. Count THREE parts BACKWARDS from five-sixths. What fraction do we land on? Two-sixths. Five-sixths minus three-sixths is two-sixths. Finally, simplify the answer if possible. To simplify fractions, find a common factor for the numerator and denominator. Two-sixths can be simplied by dividing the numerator and denominator by TWO, making the fraction one-third. Now that we have looked at the steps needed to subtract fractions on a number line, let's help Axel and Tank calculate how much petrol they have left in their submarine! Axel and Tank started their journey with the petrol tank seven eighths full in their submarine. The petrol level has dropped by six eigths. With the number line ready, what is the first step? First, check that the fractions have the same, or common, denominators. They do, as both fractions have eight as a denominator. What is the next step? Divide the number line into equal parts between whole numbers as shown by the denominator, which is EIGHT, and label each part on the number line. What should we do next? Find the first fraction, seven-eighths, which is HERE. How do we find the answer? Identify the numerator of the fraction we are subtracting, which is SIX. Count SIX parts BACKWARDS from seven-eighths. Seven-eighths minus six-eighths is one-eighth.
Can one-eighth be simplified? One-eighth CANNOT be simplified. We leave the answer as one-eighth. While Axel and Tank continue their submarine adventure, let's review! Remember, when subtracting fractions on a number line, first, check that the fractions have the same, or common, denominators. Next, divide the number line into equal parts as shown by the DENOMINATORS. Then, locate the first fraction on the number line. Finally, count backwards the number of parts as shown by the numerator of the fraction being subtracted for the answer. Remember to simplify the fraction if you can.
"Oh no! I can't believe we ran out of petrol!" "It's okay Tank, I'll go and get some more." "Fine, but please hurry up, I don't know where we are!"
Subtracting Fractions on a Number Line exercise
-
How do we subtract fractions on a number line?
HintsWhat must be checked before you divide your number line?
Where do we start jumping back from? By what do we jump backwards?
Solution- Check the fractions have the same denominator.
- Divide the number line into equal parts.
- Locate the first fraction on the number line.
- Find the numerator of the fraction being subtracted and jump backwards by this many.
- Don't forget to simplify your answer if needed.
-
How much petrol will Axel and Tank have left?
HintsCount how many parts the number line is divided into. Use the markers on the number line, and the numbers that are already there, to help you to place the fractions in the correct places.
Some of the fractions have been filled in here, so use this number line to help you fill in the rest.
Once you have a complete number line, locate the larger fraction $\frac{6}{7}$, and count backwards with the numerator of the smaller fraction.
SolutionAxel and Tank will have $\mathbf{\frac{2}{7}}$ of a tank left after their journey.
Once we placed each fraction on the number line we needed to:
- Locate the larger fraction from our equation, $\frac{6}{7}$.
- Count backwards 4 (the numerator of the smaller fraction, $\frac{4}{7}$).
- As we can see from the jumps, this takes us to $\frac{2}{7}$.
-
How much chocolate is left?
HintsThe number sentence we are trying to solve is $\frac{9}{10}$ - $\frac{6}{10}$. Can you draw a number line to help?
A number line split into tenths like this will help.
Use the number line to locate the first fraction, $\frac{9}{10}$. What is your next step?
Find the numerator in $\frac{6}{10}$ and count that many backwards.
SolutionAxel will have $\mathbf{\frac{3}{10}}$ of the chocolate bar left.
- Locate the larger fraction, $\frac{9}{10}$, on the number line.
- Find the numerator of the smaller fraction. The numerator in $\frac{6}{10}$ is 6.
- Count 6 jumps backwards.
- We land on $\frac{3}{10}$.
-
Find the answers to these subtraction problems.
HintsLook at the denominators of the fractions in the equations. Can you make a number line with this many parts to help you to subtract?
For example, to solve $\frac{7}{10}$ - $\frac{3}{10}$, we could divide a number line into 10 equal parts like this.
Once we have done that, we can locate the first fraction and count backwards by the numerator of the second fraction.
Remember, answers are simplified if needed. For example, we could simplify $\frac{2}{8}$ to $\frac{1}{4}$ by dividing both the numerator and denominator by 2.
Solution$\frac{7}{10}$ - $\frac{3}{10}$ = $\frac{2}{5}$
- Counting 3 jumps backwards from $\frac{7}{10}$ on a number line gets us to $\frac{4}{10}$.
- $\frac{4}{10}$ can be simplified to $\frac{2}{5}$ by dividing both the numerator and the denominator by 2.
$\frac{5}{6}$ - $\frac{3}{6}$ = $\frac{1}{3}$
- Counting 3 jumps backwards from $\frac{5}{6}$ on a number line gets us to $\frac{2}{6}$.
- $\frac{2}{6}$ can be simplified to $\frac{1}{3}$ by dividing both the numerator and the denominator by 2.
$\frac{7}{9}$ - $\frac{5}{9}$ = $\frac{2}{9}$
- Counting 5 jumps backwards from $\frac{7}{9}$ on a number line gets us to $\frac{2}{9}$. This cannot be simplified further.
$\frac{8}{12}$ - $\frac{2}{12}$ = $\frac{1}{2}$
- Counting 2 jumps backwards from $\frac{8}{12}$ on a number line gets us to $\frac{6}{12}$.
- $\frac{6}{12}$ can be simplified to $\frac{1}{2}$ by dividing both the numerator and the denominator by 6.
-
How much petrol will be left?
HintsThe first step is to locate the larger fraction, $\frac{5}{8}$, on the number line.
We then need to find the numerator of the smaller fraction. What is the numerator in $\frac{3}{8}$?
We then need to jump backwards that amount.
SolutionThey will have $\mathbf{\frac{2}{8}}$ of a tank of petrol left when they get home.
- Locate the larger fraction, $\frac{5}{8}$ on the number line.
- Find the numerator of the smaller fraction. The numerator of $\frac{3}{8}$ is 3.
- Count backwards 3 from $\frac{5}{8}$.
- We land on $\frac{2}{8}$.
-
What fraction will be left?
HintsMake sure the denominators are the same in each equation.
For example if we were subtracting $\frac{5}{12}$ - $\frac{2}{6}$, we would multiply the numerator and the denominator of $\frac{2}{6}$ by 2 to make $\frac{4}{12}$. Now we can subtract $\frac{5}{12}$ - $\frac{4}{12}$.
Draw your own number line to help you to solve. Divide your number line into equal parts as shown by the denominators.
Remember to simplify your answer by dividing the numerator and denominator by the same number.
Solution$\mathbf{\frac{1}{2}}$
- $\frac{9}{10}$ - $\frac{2}{5}$ : first convert the fraction, $\frac{2}{5}$, by multiplying the numerator and denominator by 2 to make $\frac{4}{10}$, so both fractions in the equation have the same denominator.
- $\frac{9}{10}$ - $\frac{4}{10}$ = $\frac{5}{10}$ which can be simplified to $\frac{1}{2}$ by dividing both the numerator and denominator by 5.
- $\frac{7}{8}$ - $\frac{3}{8}$ = $\frac{4}{8}$ which can be simplified to $\frac{1}{2}$ by dividing both the numerator and denominator by 4.
- $\frac{12}{14}$ - $\frac{5}{14}$ = $\frac{7}{14}$ which can be simplified to $\frac{1}{2}$ by dividing both the numerator and denominator by 7.
$\mathbf{\frac{2}{3}}$
- $\frac{5}{6}$ - $\frac{1}{6}$ = $\frac{4}{6}$ which can be simplified to $\frac{2}{3}$ by dividing both the numerator and denominator by 2.
- $\frac{11}{12}$ - $\frac{1}{4}$ : first convert the fraction, $\frac{1}{4}$, by multiplying the numerator and denominator by 3 to make $\frac{3}{12}$, so both fractions in the equation have the same denominator. $\frac{11}{12}$ - $\frac{3}{12}$ = $\frac{8}{12}$ which can be simplified to $\frac{2}{3}$ by dividing both the numerator and denominator by 4.
$\mathbf{\frac{3}{5}}$
- $\frac{13}{15}$ - $\frac{4}{15}$ = $\frac{9}{15}$ which can be simplified to $\frac{3}{5}$ by dividing both the numerator and denominator by 3.
- $\frac{17}{20}$ - $\frac{5}{20}$ = $\frac{12}{20}$ which can be simplified to $\frac{3}{5}$ by dividing both the numerator and denominator by 4.
Adding Fractions
Adding Tenth and Hundredth

Adding Tenth and Hundredth — Let's Practise!
Adding Fractions on a Number Line
Adding Fractions on a Number Line- Let's Practise!
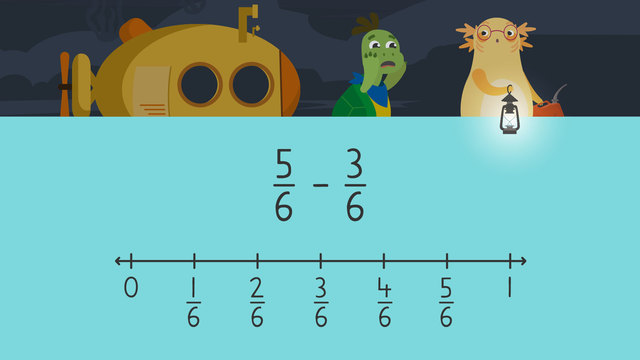
Subtracting Fractions on a Number Line
Subtracting Fractions on a Number Line — Let's Practise
Adding and Subtracting Mixed Numbers

Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise!

Adding Fractions with Different Denominators
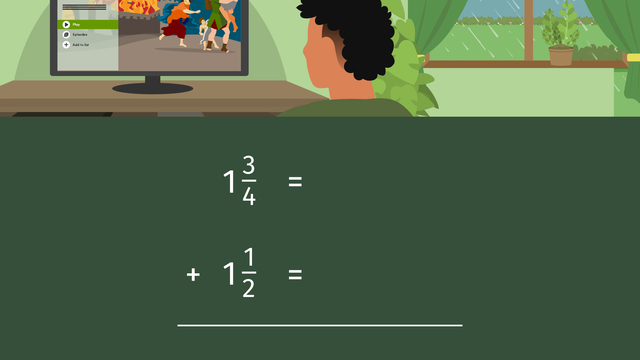
Adding Mixed Numbers with Unlike Denominators
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?













