Adding Tenth and Hundredth — Let's Practise!


Basics on the topic Adding Tenth and Hundredth — Let's Practise!
Adding Tenths and Hundredths – Introduction
We're diving into the world of adding tenths and hundredths. These problems require us to work with fractions that have different denominators. As we embark on this mathematical journey, remember that solving these problems is like unravelling a mystery, and you're the detective!
What Are Tenths and Hundredths?
Tenths and hundredths are fractions where the denominator, the bottom number, is 10 or 100. To add fractions with different denominators, we need to convert them to have the same denominator. This process involves multiplying or dividing the numerators and denominators to create equivalent fractions.
Here are the steps to tackle adding tenths and hundredths:
| Step # | Action |
|---|---|
| 1 | Read the problem and determine what you are asked to find. |
| 2 | Identify the fractions and their denominators. |
| 3 | Convert the fractions to have a common denominator. |
| 4 | Add the fractions. |
| 5 | Simplify the fraction if necessary. |
| 6 | Check your answer to ensure it makes sense with the problem. |
Let's practise understanding tenths and hundredths problems with a couple of exercises.
Solving Tenths and Hundredths Problems – Example
Example 1:
Problem: Solve $\frac{35}{100} + \frac{3}{10}$.
Steps to Solve the Problem:
| Step # | Action | Equation |
|---|---|---|
| 1 | Write an equation for the problem. | $\frac{35}{100}$ + $\frac{3}{10}$ |
| 2 | Convert three-tenths to hundredths. | $\frac{3}{10} \times \frac{10}{10}$ = $\frac{30}{100}$ |
| 3 | Add the fractions. | $\frac{35}{100}$ + $\frac{30}{100}$ = $\frac{65}{100}$ |
| 4 | Combine the fractions. | $\frac{65}{100}$ |
Solution: The sum is $\frac{65}{100}$ or sixty-five hundredths.
Example 2:
Problem: Solve $\frac{3}{100} + \frac{5}{10}$.
Steps to Solve the Problem:
| Step # | Action | Equation |
|---|---|---|
| 1 | Write an equation for the problem. | $\frac{3}{100}$ + $\frac{5}{10}$ |
| 2 | Convert five-tenths to hundredths. | $\frac{5}{10} \times \frac{10}{10} = \frac{50}{100}$ |
| 3 | Add the fractions. | $\frac{3}{100} + \frac{50}{100} = \frac{53}{100}$ |
| 4 | Combine the fractions. | $\frac{53}{100}$ |
Solution: The sum is $\frac{53}{100}$ or fifty-three hundredths.
Example 3:
Problem: Solve $\frac{30}{100} + \frac{2}{10}$.
Steps to Solve the Problem:
| Step # | Action | Equation |
|---|---|---|
| 1 | Write an equation for the problem. | $\frac{30}{100} + \frac{2}{10}$ |
| 2 | Convert thirty-hundredths to tenths. | $\frac{30}{100} \div \frac{10}{10} = \frac{3}{10}$ |
| 3 | Add the fractions. | $\frac{3}{10} + \frac{2}{10} = \frac{5}{10}$ |
| 4 | Simplify the fraction if necessary. | $\frac{5}{10} = \frac{1}{2}$ |
Solution: The sum is $\frac{5}{10}$ or $\frac{1}{2}$.
Solving Tenths and Hundredths Problems – Application
Now, let's put your skills to the test. Solve these problems on your own, and check the solutions when you're ready!
Solving Tenths and Hundredths Problems – Summary
Key Learnings from this Text:
- Solving problems with tenths and hundredths can be achieved by following these steps:
| Step # | Action |
|---|---|
| 1 | Read the problem and determine what you are asked to find. |
| 2 | Identify the fractions and their denominators. |
| 3 | Convert the fractions to have a common denominator. |
| 4 | Add the fractions. |
| 5 | Simplify the fraction if necessary. |
| 6 | Check your answer to ensure it makes sense with the problem. |
- Mastering addition with tenths and hundredths is an important foundational maths skill.
Keep practising these steps, and you'll become a pro at solving tenths and hundredths problems! Check out more fun maths challenges and exercises on our website to continue sharpening your skills.
Solving Tenths and Hundredths Problems – Frequently Asked Questions
Transcript Adding Tenth and Hundredth — Let's Practise!
Razzi says get these items ready because today we're going to practise adding tenths and hundredths. It's time to begin! Solve thirty-five hundredths plus three tenths. Pause the video to work on the problem and press play when you are ready to see the solution! We need the denominators to be the same to add. Start by converting three tenths. Multiply the numerator and denominator by ten to get thirty hundredths. We now know that our answer will have the same denominator. Thirty-five plus thirty equals sixty-five. Did you also get sixty-five hundredths? Let's tackle the next problem! Solve three hundredths plus five tenths. Pause the video to work on the problem and press play when you are ready to see the solution! We need the denominators to be the same to add. Start by converting five tenths. Multiply the numerator and denominator by ten to get fifty hundredths. Then, write one hundred as the denominator in the answer. Three plus fifty equals fifty-three. Did you also get fifty-three hundredths? Let's tackle the final problem! Solve thirty hundredths plus two tenths. This time, convert thirty hundredths to tenths! Pause the video to work on the problem and press play when you are ready to see the solution! Start by converting thirty hundredths to tenths. Divide the numerator and denominator by ten to get three tenths. Therefore, this time, ten will be the denominator in the answer. Three plus two equals five. Five tenths can be simplified to one half! Did you also get five tenths or one half? Razzi had so much fun practising with you today! See you next time!
Adding Tenth and Hundredth — Let's Practise! exercise
-
Identify the expressions that are equivalent.
HintsTo compare the expressions, you must first create like-denominators.
The fractions, $\frac{55}{100}$ and $\frac{3}{100}$ share like denominators. The fractions, $\frac{55}{100}$ and $\frac{3}{10}$ do not.
SolutionWhen you add tenths and hundredths, you need to first make sure the denominators are the same. By multiplying the numerator and the denominator of $\frac{3}{10}$ you make $\frac{30}{100}$, which you can then add to $\frac{35}{100}$. The same applies with $\frac{5}{10}$, $\frac{3}{10}$, and $\frac{4}{10}$.
- $\frac{3}{10}$ x 10 = $\frac{30}{100}$ = $\frac{35}{100}$ + $\frac{30}{100}$
- $\frac{5}{10}$ x 10 = $\frac{50}{100}$ = $\frac{3}{100}$ + $\frac{50}{100}$
- $\frac{6}{10}$ x 10 = $\frac{60}{100}$ = $\frac{60}{100}$ + $\frac{2}{100}$
- $\frac{4}{10}$ x 10 = $\frac{40}{100}$ = $\frac{40}{100}$ + $\frac{45}{100}$
-
Can you answer the questions?
HintsTo compare the expressions, you must first create like-denominators.
$\frac{30}{100}$ would become $\frac{3}{10}$, which we could then add to $\frac{2}{10}$.
The fractions, $\frac{55}{100}$ and $\frac{3}{100}$ share like denominators. The fractions, $\frac{55}{100}$ and $\frac{3}{10}$ do not.
When creating like denominators don't forget to divide or multiply the numerator as well!
Once you have converted one fraction in the equation, add the numerators to find the answer.
Solution- $\frac{50}{100}$ ÷ 10 = $\frac{5}{10}$. We can then add this to $\frac{3}{10}$ to get $\frac{8}{10}$.
- $\frac{20}{100}$ ÷ 10 = $\frac{2}{10}$. We can then add this to $\frac{5}{10}$ to get $\frac{7}{10}$.
- $\frac{40}{100}$ ÷ 10 = $\frac{4}{10}$. We can then add this to $\frac{5}{10}$ to get $\frac{9}{10}$.
- $\frac{10}{100}$ ÷ 10 = $\frac{1}{10}$. We can then add this to $\frac{5}{10}$ to get $\frac{6}{10}$.
-
Solve the equations.
HintsUse a pencil and paper to help you keep track of the steps.
With the equation, $\frac{35}{100}$ + $\frac{3}{10}$, and $\frac{3}{100}$ + $\frac{5}{10}$, it is easiest to multiply to create common denominators.
With the equation, $\frac{30}{100}$ + $\frac{2}{10}$, it is easiest to divide to create common denominators.
Solution- $\frac{35}{100}$ + $\frac{3}{10}$ = $\frac{35}{100}$ + $\frac{30}{100}$ = $\frac{65}{100}$
- $\frac{3}{100}$ + $\frac{5}{10}$ = $\frac{3}{100}$ + $\frac{50}{100}$ = $\frac{53}{100}$
- $\frac{30}{100}$ + $\frac{2}{10}$ = $\frac{3}{10}$ + $\frac{2}{10}$ = $\frac{5}{10}$ or $\frac{30}{100}$ + $\frac{2}{10}$ = $\frac{30}{100}$ + $\frac{20}{100}$ = $\frac{50}{100}$
-
What is $\frac{40}{100}$ + $\frac{4}{10}$?
HintsFirst, divide the numerator and denominator of $\frac{40}{100}$ and fill in the new addition equation.
Answer the addition equation. How can this answer be simplified?
As an example, the answer to this equation is $\frac{5}{10}$, which can be simplified to $\frac{1}{2}$ by dividing both the numerator and denominator by 5.
Solution$\frac{40}{100}$ + $\frac{4}{10}$ = $\mathbf{\frac{4}{10}}$ + $\mathbf{\frac{4}{10}}$ = $\mathbf{\frac{8}{10}}$ = $\mathbf{\frac{4}{5}}$
If we divide the numerator and denominator of $\frac{8}{10}$ by 2, we get $\mathbf{\frac{4}{5}}$.
Alternatively
$\frac{40}{100}$ + $\frac{4}{10}$ = $\mathbf{\frac{40}{100}}$ + $\mathbf{\frac{40}{100}}$ = $\mathbf{\frac{80}{100}}$ = $\mathbf{\frac{4}{5}}$
If we divide the numerator and denominator of $\frac{80}{100}$ by 20, we get $\mathbf{\frac{4}{5}}$.
-
What is $\frac{7}{10}$ + $\frac{8}{100}$?
HintsAlways remember to multiply both the numerator (above) and denominator (below) by the same number.
We first need to convert $\frac{7}{10}$ to hundredths by multiplying the numerator and denominator by 10.
$\frac{7}{10}$ = $\frac{70}{100}$
Now we can add $\frac{70}{100}$ + $\frac{8}{100}$
Solution$\frac{7}{10}$ + $\frac{8}{100}$ = $\mathbf{\frac{70}{100}}$ + $\frac{8}{100}$ = $\mathbf{\frac{78}{100}}$
-
Solve the equations.
HintsTo answer the equations, first convert one so that both fractions in the equation have common denominators.
Remember to simplify as many times as necessary.
For example, $\frac{40}{100}$ can be simplified to $\frac{2}{5}$ by dividing both the numerator and denominator by 20.
Solution- $\frac{20}{100}$ + $\frac{5}{10}$ = $\frac{2}{10}$ + $\frac{5}{10}$ = $\frac{7}{10}$ or $\frac{20}{100}$ + $\frac{5}{10}$ = $\frac{20}{100}$ + $\frac{50}{100}$ = $\frac{7}{10}$
- $\frac{30}{100}$ + $\frac{2}{10}$ = $\frac{3}{10}$ + $\frac{2}{10}$ = $\frac{5}{10}$ = $\frac{1}{2}$ or $\frac{30}{100}$ + $\frac{2}{10}$ = $\frac{30}{100}$ + $\frac{20}{100}$ = $\frac{50}{100}$ = $\frac{1}{2}$
- $\frac{3}{10}$ + $\frac{50}{100}$ = $\frac{3}{10}$ + $\frac{5}{10}$ = $\frac{8}{10}$ = $\frac{4}{5}$ or $\frac{3}{10}$ + $\frac{50}{100}$ = $\frac{30}{100}$ + $\frac{50}{100}$ = $\frac{80}{100}$ = $\frac{4}{5}$
- $\frac{4}{10}$ + $\frac{20}{100}$ = $\frac{4}{10}$ + $\frac{2}{10}$ = $\frac{6}{10}$ = $\frac{3}{5}$ or $\frac{4}{10}$ + $\frac{20}{100}$ = $\frac{40}{100}$ + $\frac{20}{100}$ = $\frac{60}{100}$ = $\frac{3}{5}$
Adding Fractions
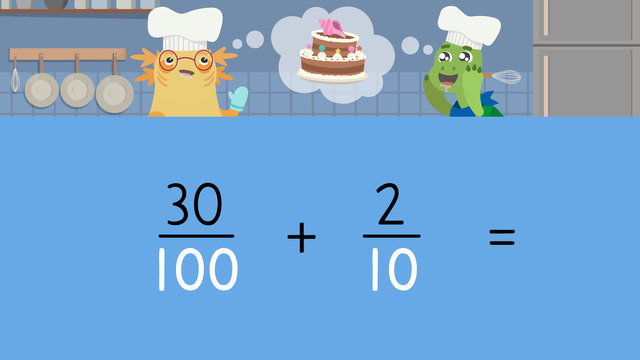
Adding Tenth and Hundredth

Adding Tenth and Hundredth — Let's Practise!
Adding Fractions on a Number Line
Adding Fractions on a Number Line- Let's Practise!
Subtracting Fractions on a Number Line
Subtracting Fractions on a Number Line — Let's Practise
Adding and Subtracting Mixed Numbers

Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise!

Adding Fractions with Different Denominators
Adding Mixed Numbers with Unlike Denominators
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?









