Adding Fractions
Basics on the topic Adding Fractions
Adding Fractions with the Same Denominator
When adding fractions does the denominator change? This text will show how when adding fractions together, it is only the numerators that we add whilst the denominator stays the same.
Adding Fractions – Rules
These are the steps to follow when adding fractions:
| Step # | What to do |
|---|---|
| 1 | Check that the denominators are the same, and write it in the total. |
| 2 | Add the numerators. |
| 3 | Write the numerator above the denominator in the total. |
If you follow these adding fractions rules you will be able to solve adding fractions word problems as well as more straightforward adding fractions questions.
Adding Fractions – Example
Let’s take a look at an example of adding fractions with the same denominator and find out if when adding fractions does the denominator change? Here, we’ll add five-tenths plus three-tenths following the adding fractions rules.
Step 1: Check that the denominators are the same, and write it in the total
Step 2: Add the numerators


Can you simplify when adding fractions? As shown in this example, yes we can, as we simplified eight-tenths to four-fifths.
Adding Fractions with the Same Denominator – Summary
When adding fractions with like denominators, we keep in mind these rules for adding fractions. There are steps to adding fractions which should be followed:
- Step 1: Double check that the denominators are the same, and write it in the total
- Step 2: Add the numerators
- Step 3: Write the numerator above the denominator in the total
Want some more adding fractions practise? After watching this video on this website you can find adding fractions with the same denominator worksheet along with other activities, and exercises.
Transcript Adding Fractions
Can you hear that sound? It sounds like Ophelia, the sea witch, crying inside of her lair! Axel and Tank need to know what the fuss is about and they find that Ophelia is trying to get ready for a party, but has made a big mess! She needs help counting the jellyfish, starfish and sea urchin decorations she is painting for a party. Let's practise adding fractions with the same denominator to count the decorations she is painting. A fraction describes parts of a whole or parts of an amount. The top part of the fraction is the numerator, it represents how many equal parts our whole is divided into. The bottom part of the fraction is the denominator, it represents how equal parts there are in the whole. To start, Ophelia paints three out of seven, or three-sevenths, of her jellyfish orange. If she paints two more, how many jellyfish will be painted in total? We can find the total by solving the equation three-sevenths plus two-sevenths. When you add fractions with the same denominator, the denominator always stays the same as the number of parts in our whole does not change. That is why our first step is to check the denominators to make sure that they are the same. Since the fractions have the same denominator we can write the denominator of our total here. The second step is to add the numerators. Three plus two is five, and we write it here. That means five-sevenths of Ophelia's jellyfish will be painted orange. Next, she paints five-tenths of the starfish yellow. If she paints three more, how many starfish will be painted in total? This time we will add five-tenths plus three-tenths. What is the first step? First, check that the denominators are the same and write ten here. What is the second step? The second step is to add the numerators. What is five plus three? The sum is eight. Eight-tenths can be simplified to four-fifths which means, eight-tenths or four-fifths of Ophelia's starfish will be painted yellow. Finally, she paints four-twelfths of the sea urchins red and she will paint eight more. What is four-twelfths plus eight-twelfths? First, check that the denominators are the same, and write twelve here. Next, add four plus eight to get twelve. Twelve twelfths can be simplified to one whole, which means Ophelia will paint all of her sea urchins red! Remember, when adding fractions with the same denominator. The first step is to make sure that the denominators are the same and write it in the total. When you add fractions with the same denominator, the denominators always stay the same and do not get added. The second step is to add the numerators. The third step is to write the numerator above the denominator in the total, simplifying the fraction where you need to. Let's see how Ophelia's party turned out! Looks like she's the light of the party!
Adding Fractions exercise
-
Adding fractions.
HintsRemember that when we add fractions with the same denominator, we only need to look at the numerators and add these.
When we add fractions with the same denominator, this stays the same.
Solution- $\frac{4}{12}$ + $\frac{6}{12}$ = $\frac{10}{12}$
- $\frac{3}{10}$ + $\frac{5}{10}$ = $\frac{8}{10}$
- $\frac2 7$ + $\frac1 7$ = $\frac3 7$
- $\frac3 9$ + $\frac5 9$ = $\frac8 9$
-
Add the fractions of shells.
HintsThe denominator is how many parts (shells) we have in total. It always remains the same.
How many shells have been painted in each colour? This is our numerator as it is the parts of the whole.
SolutionThere are 8 shells in total, so this is our denominator.
3 out of 8 are painted yellow, this is $ \frac3 8$.
2 out of 8 are painted red, this is $ \frac2 8$.
In total, there are 5 out of 8 painted, $ \frac5 8$.
-
Painted shells.
HintsRemember that when we find fractions of amounts, the total amount in the group is the denominator (the bottom part of the fraction). In this image there are 5 shells in total, so the denominator would be 5.
The parts that we are counting (here, the painted shells) is the numerator. In this example it is 3.
SolutionThere are 6 shells in total. 3 are painted purple and 2 are painted red. The fraction of shells that have been painted is $\mathbf{\frac{5}{6}}$
To find the total fraction of shells that have been painted, we need to add $\mathbf{\frac{2}{8}}$ and $\mathbf{\frac{3}{8}}$ to get $\mathbf{\frac{5}{8}}$
There are 5 shells in total. $\mathbf{\frac{1}{5}}$ + $\mathbf{\frac{2}{5}}$ = $\mathbf{\frac{3}{5}}$.
-
Pizza fractions.
HintsRemember that when we add fractions with the same denominator, we only add the numerators together. The denominator stays the same.
How many slices was each pizza originally cut into? This is your denominator.
How many slices are left? This is the numerator. In this example there is one slice left out of four, so $\frac1 4$ remains.
SolutionThe image shows the answer to the pepperoni pizza:
$\frac3 8$ + $\frac4 8$ = $\frac7 8$.
Mushroom pizza:
$\frac2 6$ + $\frac3 6$ = $\frac5 6$.
Olive pizza:
$\frac2 5$ + $\frac2 5$ = $\frac4 5$.
Cheese pizza:
$\frac4 8$ + $\frac2 8$ = $\frac6 8$.
-
Fractions of fish.
HintsWhen we are trying to find $ \frac4 7$ of an amount, we know that there are 7 items in total as this is the denominator.
What is the numerator? This is how many out of the total that are colourful. In this example, the numerator is 4.
SolutionThe tank with $ \frac4 7$ of the fish being colourful, is the tank with 7 fish in the tank - this is the denominator - and 4 fish coloured in the tank (3 orange and 1 yellow fish) - this is the numerator.
-
Add fractions.
HintsRemember that we can simplify fractions by dividing the numerator and the denominator by the same factor, to find an equivalent fraction.
Here $ \frac2 4$ has been simplified to $ \frac1 2$ by dividing the numerator and the denominator by 2.
Solution$\mathbf{\frac{2}{3}}$
- $\frac1 3$ + $\frac1 3$ = $\frac2 3$.
- $\frac2 6$ + $\frac2 6$ = $\frac4 6$ .
- We can simplify $\frac4 6$ to $\frac2 3$ by dividing both the numerator and denominator by 2.
$\mathbf{\frac{1}{2}}$
- $\frac2 8$ + $\frac2 8$ = $\frac4 8$.
- We can simplify $\frac4 8$ to $\frac1 2$ by dividing both the numerator and denominator by 4.
- $\frac{4}{10}$ + $\frac{1}{10}$ = $\frac{5}{10}$.
- We can simplify $\frac{5}{10}$ to $\frac1 2$ by dividing both the numerator and denominator by 5.
$\mathbf{\frac{4}{5}}$
- $\frac3 5$ + $\frac1 5$ = $\frac4 5$.
- $\frac{6}{10}$ + $\frac{2}{10}$ = $\frac{8}{10}$.
- We can simplify $\frac{8}{10}$ to $\frac4 5$ by dividing both the numerator and denominator by 2.
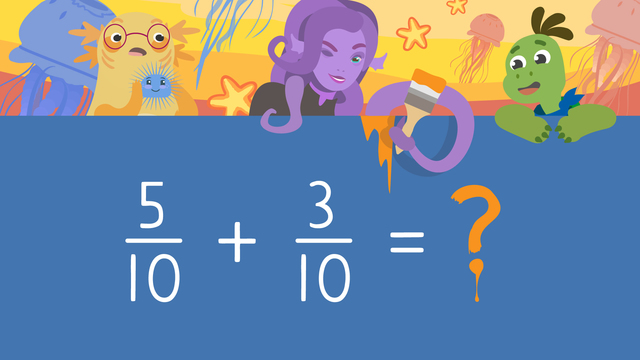
Adding Fractions
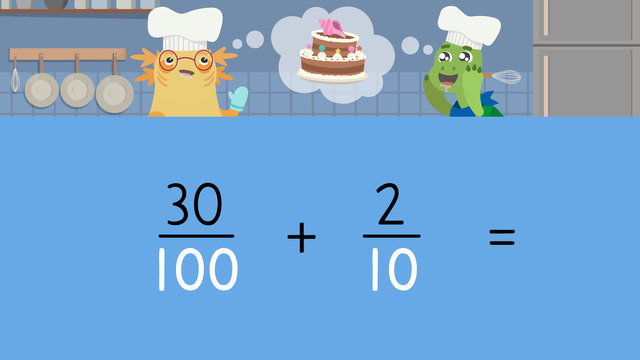
Adding Tenth and Hundredth

Adding Tenth and Hundredth — Let's Practise!
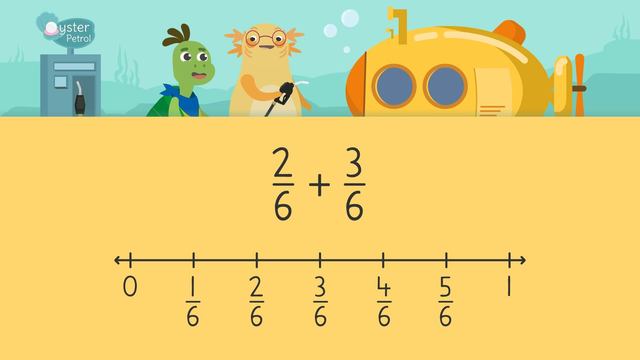
Adding Fractions on a Number Line
Adding Fractions on a Number Line- Let's Practise!
Subtracting Fractions on a Number Line
Subtracting Fractions on a Number Line — Let's Practise
Adding and Subtracting Mixed Numbers

Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise!

Adding Fractions with Different Denominators
Adding Mixed Numbers with Unlike Denominators

 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?











