Adding Fractions on a Number Line- Let's Practise!

Basics on the topic Adding Fractions on a Number Line- Let's Practise!
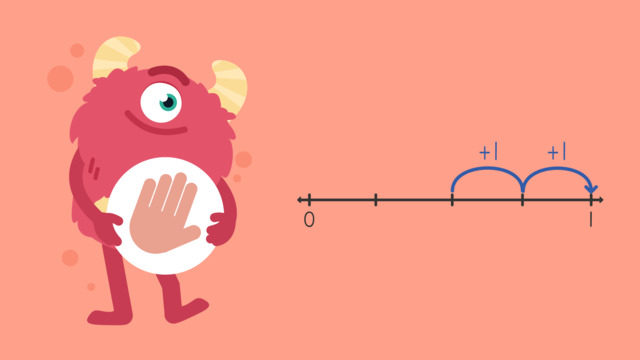
Let's learn all about, how to add fractions using a number line!
Transcript Adding Fractions on a Number Line- Let's Practise!
Razzi says get these items ready because today we're going to practise adding fractions on a number line. It's time to begin! Using a number line solve two-sixths plus three-sixths. Pause the video to work on the problem and press play when you are ready to see the solution! Both denominators are six, so divide the number line into six equal parts and label them. Locate two-sixths which is here. Count forward the numerator of the second fraction which is three. Did you also get five-sixths? Let's tackle the next problem! Using a number line solve two-quarters plus two-quarters. Pause the video to work on the problem and press play when you are ready to see the solution! Both denominators are four, so divide the number line into four equal parts and label them. Locate two-quarters which is here. Count forward the numerator of the second fraction which is two. Did you also get four-quarters or one whole? Let's tackle the final problem! Using a number line solve one-eighth plus five-eighths. Pause the video to work on the problem and press play when you are ready to see the solution! Both denominators are eight, so divide the number line into eight equal parts and label them. Locate one-eighth which is here. Count forward the numerator of the second fraction, which is five. We land on six-eighths, which can be simplified to three-quarters. Did you also get six-eighths or three-quarters? Razzi had so much fun practising with you today! See you next time!
Adding Fractions on a Number Line- Let's Practise! exercise
-
Add the fractions.
HintsWhat is the first fraction you are adding? Start here on the number line.
Look at the numerator of the second fraction you are adding, count forward by this amount.
Solution$\mathbf{\frac{2}{5}}$ + $\mathbf{\frac{2}{5}}$ = $\mathbf{\frac{4}{5}}$ When we add fractions, we only add the numerators and the denominator stays the same.
- We start at $\mathbf{\frac{2}{5}}$ and count forward by $\mathbf{\frac{2}{5}}$.
- 2 + 2 = 4.
- So $\mathbf{\frac{2}{5}}$ + $\mathbf{\frac{2}{5}}$ = $\mathbf{\frac{4}{5}}$
-
Add the fractions with the same denominator.
HintsYou could start by drawing a number line and splitting it into the number of parts that is the same as the denominator.
Find the first fraction on the number line and count forward by the numerator of the second fraction.
SolutionA bucket is filled to $\mathbf{\frac{3}{8}}$, another $\mathbf{\frac{2}{8}}$ are added. Now the bucket is filled to $\mathbf{\frac{5}{8}}$.
-
Add the fractions using the number line.
HintsStart by finding the first fraction to add on the number line, this is $\frac{2}{6}$.
Then, count forwards by the numerator of the second fraction you are adding.
Solution$\mathbf{\frac{2}{6}}$ + $\mathbf{\frac{3}{6}}$ = $\mathbf{\frac{5}{6}}$
- When we add fractions, we only add the numerators and the denominator stays the same.
- We start at $\mathbf{\frac{2}{6}}$ and count forward by $\mathbf{\frac{3}{6}}$.
- 2 + 3 = 5.
- So $\mathbf{\frac{2}{6}}$ + $\mathbf{\frac{3}{6}}$ = $\mathbf{\frac{5}{6}}$
-
What is $\frac{3}{9}$ + $\frac{2}{9}$?
HintsYou could start by drawing a number line and splitting it into the number of parts that is the same as the denominator.
Start by finding the first fraction to add on the number line.
Then, count forwards by the numerator of the second fraction you are adding.
Solution$\mathbf{\frac{3}{9}}$ + $\mathbf{\frac{2}{9}}$ = $\mathbf{\frac{5}{9}}$
- When we add fractions, we only add the numerators and the denominators stay the same. 3 + 2 = 5.
- So $\mathbf{\frac{3}{9}}$ + $\mathbf{\frac{2}{9}}$ = $\mathbf{\frac{5}{9}}$
-
Add the fractions together.
HintsStart by finding the first fraction to add on the number line, then count forwards by the numerator of the second fraction.
The numerator in the second fraction to add is 2. What do you end up on when you count forward two from $\frac{5}{8}$?
Solution$\mathbf{\frac{5}{8}}$ + $\mathbf{\frac{2}{8}}$ = $\mathbf{\frac{7}{8}}$
- When we add fractions, we only add the numerators and the denominator stays the same.
- We start at $\mathbf{\frac{5}{8}}$ and count forward by $\mathbf{\frac{2}{8}}$.
- 5 + 2 = 7.
- So $\mathbf{\frac{5}{8}}$ + $\mathbf{\frac{2}{8}}$ = $\mathbf{\frac{7}{8}}$
-
What is $\frac{3}{7}$ + $\frac{4}{7}$ ?
HintsWhen we add fractions with the same denominator, the denominator stays the same and we add the numerators together.
We can simplify fractions by dividing the numerator and denominator by the same factor.
When the numerator is the same as the denominator, the fraction can be simplified to one whole.
Solution$\mathbf{\frac{3}{7}}$ + $\mathbf{\frac{4}{7}}$ = $\mathbf{\frac{7}{7}}$
- When we add fractions, we only add the numerators and the denominators stay the same. 3 + 4 = 7.
- We can simplify $\mathbf{\frac{7}{7}}$ to 1 whole by dividing the numerator and denominator by the same factor.
- When we divide $\mathbf{\frac{7}{7}}$ by 7, we get $\mathbf{\frac{1}{1}}$ which is equivalent to one whole.
Adding Fractions
Adding Tenth and Hundredth

Adding Tenth and Hundredth — Let's Practise!
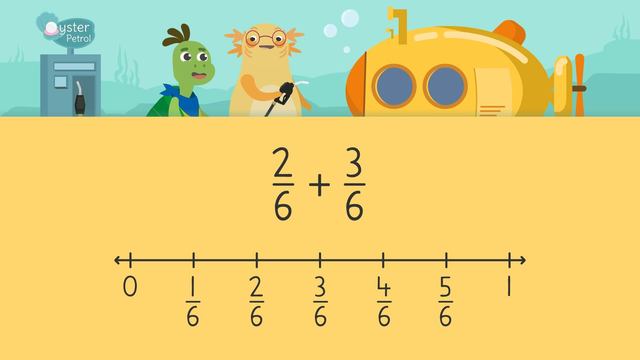
Adding Fractions on a Number Line

Adding Fractions on a Number Line- Let's Practise!
Subtracting Fractions on a Number Line
Subtracting Fractions on a Number Line — Let's Practise
Adding and Subtracting Mixed Numbers

Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise!

Adding Fractions with Different Denominators
Adding Mixed Numbers with Unlike Denominators


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?









