Multiplying Fractions
Learning text on the topic Multiplying Fractions
Multiplying Fractions
Welcome to the world of Multiplying Fractions! This fundamental maths concept is a stepping stone in understanding more complex mathematical operations. In this learning text, we'll explore what multiplying fractions involves, provide clear explanations and some practice for you to try.
Understanding Multiplying Fractions
Multiplying fractions might seem tricky at first, but it's quite straightforward once you understand the basics. All you need to do is multiply the numerators together and then multiply the denominators together!
Multiplying fractions involves multiplying the numerators (top numbers) of the fractions together and the denominators (bottom numbers) together.
Below, you will find multiplying fractions steps outlined in a table for you to copy or refer to as you work through this text. You can also remember this as the fraction multiplication rules.
| Step | Description |
|---|---|
| 1 | Multiply the numerators (the top numbers) together. |
| 2 | Multiply the denominators (the bottom numbers) together. |
| 3 | Write down the product as a new fraction. |
| 4 | Simplify the fraction if possible. |
If you cannot remember how to simplify fractions, then reviewing Simplifying Fractions will help with this topic.
Before we move on to some guided practice and examples, let’s check your understanding so far of multiplying fractions.
Multiplying Fractions – Example
Let’s look at some fraction multiplication examples to understand this concept better. Suppose you need to multiply $\frac{1}{4}$ by $\frac{3}{2}$. Here’s how you do it:
- Multiply the numerators: $1\times3$ = $3$
- Multiply the denominators: $4\times2 = 8$
- The product is $\frac{3}{8}$
$\frac{1}{4}$ x $\frac{3}{2}$ = $\frac{3}{8}$, which cannot be simplified further.
Let's look at another example. This time we will multiply $\frac{2}{3}$ by $\frac{3}{4}$. Here’s how you do it:
- Multiply the numerators: $2\times3 = 6$
- Multiply the denominators: $3\times4 = 12$
- The product is $\frac{6}{12}$
$\frac{2}{3}$ x $\frac{3}{4}$ = $\frac{6}{12}$, which can be simplified to $\frac{1}{2}$.
Multiplying Fractions – Guided Practice
Let’s walk through an example together! Let’s multiply $\frac{2}{3}$ by $\frac{1}{6}$.
Multiplying Fractions – Application
Now let’s try it on your own by doing some multiplying fractions practice!
Multiplying Fractions – Summary
- Multiplying fractions involves multiplying the numerators and denominators, then simplifying the product fraction if that is possible.
- The process is straightforward and follows a consistent pattern.
- Practice with examples helps in mastering this concept.
Explore more on this topic and related ones through our interactive practice problems, engaging videos and printable worksheets on our platform. Dive deeper into the fascinating world of fractions and enhance your mathematical skills! Ready for a challenge? Then have a go at Unit Rates with Fractions.
Frequently Asked Questions about Multiplying Fractions
Multiplying Fractions exercise
-
Place the keywords provided to fill in the gaps so that the steps to multiply fractions together are complete.
HintsThe number on the top of a fraction is called the numerator. In this example, the numerator is $1$.
The number on the bottom of a fraction is called the denominator. In this example, the denominator is $5$.
When you multiply two numbers together, the answer is called the product.
It's often best to simplify a fraction where possible as this can make it easier to handle if you have to do more calculations with it.
Solution1) Multiply the numerators (the top numbers) together.$\\$ 2) Multiply the denominators (the bottom numbers) together.$\\$ 3) Write down the product as a new fraction.$\\$ 4) Simplify the fraction if possible.$\\$
-
Multiply the Fractions together.
HintsMultiply the numerators together first. Then multiply the denominators together second.
You don't need to simplify in this question so focus entirely on the method of how to multiply fractions.
Incorrect answers in this task often stem from common mistakes when multiplying fractions, such as adding numerators or denominators or cross multiplying. These errors may give results close to the correct ones. Beware of being misled by these incorrect answers!
Solution$\frac{3}{5} \times \frac{2}{3} = \frac{6}{15}$
$\frac{4}{7} \times \frac{3}{4} = \frac{12}{28}$
$\frac{2}{9} \times \frac{5}{6} = \frac{10}{54}$
$\frac{3}{8} \times \frac{2}{5} = \frac{6}{40}$
-
Complete the calculation
HintsLook at this example. Notice how the two numerators have been multiplied to give the answer numerator. Then the two denominators have been multiplied to get the answer denominator.
In this worked example, the multiplication has been completed and then the answer has been simplified to show you there is often more than one correct answers to a problem.
Sometimes, the numbers on the top and bottom of the fractions have factors in common. If they do, you can divide both numbers by the same factor to simplify your answer.
Solution$\frac{2}{7} \times \frac{3}{4} = \frac{6}{28}$
This can be simplified to be $\frac{3}{14}$
$\frac{3}{14}$ is the simplified answer as the numerator and denominator of $\frac{6}{28}$ have been divided by $2$.
-
Sort the answers.
HintsBreak the question down into parts. First complete the multiplication calculations. Then simplify your answers if possible. Finally sort them into size order, smallest to largest.
When organising answers by size, multiple methods can be used. One way is to draw circles, dividing each into slices based on the denominator and colouring in the number of slices indicated by the numerator. Then, compare the level of colouring in each circle to determine the order of the answers from smallest to largest.Have a look at the image to help you with this.
Convert fractions to decimals for an easier comparison and sorting method. Watch our video tutorial on this if you need a refresher on how to do this.
Look at the following worked example to demonstrate how you can break this problem down into smaller steps to help you complete it.
Question - $\frac{1}{3} \times \frac{3}{4}$
Step 1 - Multiply the fractions. $\frac{1}{3} \times \frac{3}{4} = \frac{3}{12}$.
Step 2 - Simplify your answer if possible. $\frac{3}{12}$ simplifies to become $\frac{1}{4}$.
Step 3 - Convert your answer to a form you feel confident comparing in. You can convert $\frac{1}{4}$ to a diagram like the one included with this hint for helping you visually see how much of a whole the fraction represents. You could also convert $\frac{1}{4}$ to the decimal $0.25$ if you prefer comparing decimals using place value.
SolutionSmallest
- $\frac{2}{5} \times \frac{1}{2} = \frac{2}{10}$
- $\frac{2}{5} \times \frac{3}{4} = \frac{6}{20}$
- $\frac{4}{5} \times \frac{5}{8} = \frac{20}{40}$
- $\frac{10}{25} \times \frac{4}{2} = \frac{40}{50}$
Largest
To show these fractions visually, look at the image. Each of the fractions has been simplified to get a common denominator. Then a circle has been divided into the number of parts given in the denominator and each segment has been shaded to match the numerator of the fraction. By seeing the fractions visually like this we can easily compare them and see which is the smallest and which is the largest.
$\frac{2}{10}$
$\frac{6}{20} = \frac{3}{10}$
$\frac{20}{40} = \frac{5}{10}$
$\frac{40}{50} = \frac{8}{10}$
-
Multiply the fractions together.
HintsTo multiply fractions, you need to multiply the numbers on the top (numerator) together and then the numbers on the bottom (denominator). It's like doing two separate little math problems!
Sometimes, the numbers on the top and bottom of the fractions have factors in common. If they do, you can divide both numbers by the same factor to simplify your answer.
Sometimes you will be able to simplify a fraction multiple times before you cannot simplify it any further.
Solution$\frac{2}{3} \times \frac{3}{4} = \frac{6}{12}$ which simplifies to $\frac{1}{2}$
$\frac{1}{2} \times \frac{2}{5} = \frac{2}{10}$ which simplifies to $\frac{1}{5}$
$\frac{3}{8} \times \frac{4}{5} = \frac{12}{40}$ which simplifies to $\frac{3}{10}$
$\frac{2}{3} \times \frac{2}{5} = \frac{4}{15}$
-
Apply your knowledge on multiplying fractions.
HintsThe method for multiplying fractions is always the same. Multiply the numerators together and then multiply your denominators together.
Could you try some examples to test out the statements? For example do the solutions to the calculation $\frac{1}{2} \times \frac{1}{2}$ and then $\frac{2}{3} \times \frac{3}{4}$ help you with one of the statements?
A proper fraction is a fraction where the numerator is less than the denominator. An example would be $\frac{2}{5}$. An improper fraction is a fraction where the numerator is greater than or equal to the denominator. An example would be $\frac{7}{4}$.
Solution- Always - When multiplying fractions, you multiply the numerators together to get the new numerator, and you multiply the denominators together to get the new denominator. An example would be $\frac{2}{5} \times \frac{1}{3} = \frac{2}{15}$
- Sometimes - The product of two fractions is smaller than one of the original fractions. An example where this is true is $\frac{1}{4} \times \frac{1}{2} = \frac{1}{8}$. An example where this is not true is $\frac{4}{3} \times \frac{3}{2} = \frac{12}{6}$
- Sometimes - The product of two fractions is equal to one of the original fractions.An example where this is true is $\frac{1}{4} \times \frac{1}{1} = \frac{1}{4}$.
- Never - The product of two proper fractions is an improper fraction.

Fractions as a Multiple of Unit Fractions
Multiplying a Fraction by a Whole Number

Multiplying Fractions Less Than One
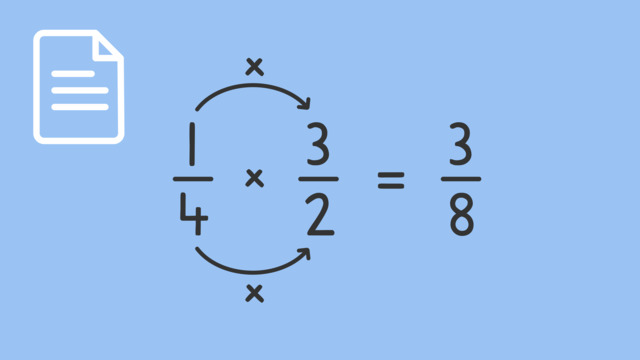
Multiplying Fractions
Dividing Fractions
Ratios of Fractions

Dividing Whole Numbers by Unit Fractions Using Models

Lowest Common Multiples

Multiplying Mixed Numbers: Word Problems

Finding the Greatest Common Factor
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?











