Fractions as a Multiple of Unit Fractions


Basics on the topic Fractions as a Multiple of Unit Fractions
Unit Fractions
When we have more than one unit fraction, we have multiple unit fractions, for example if we had four lots of $\frac{1}{5}$, we would have $\frac{4}{5}$.
Unit Fractions – Definition
Unit and non unit fractions are different. Here, you can learn all about unit fractions and how to find multiples of unit fractions. A unit fraction is one part of a whole that is divided into equal parts. A unit fraction has 1 as the top number (the numerator), which is the numerator. The bottom number (denominator) indicates the number of parts in which the whole was split. If the denominator is 5, our unit fraction is $\frac{1}{5}$.
| Term | Example |
|---|---|
| numerator | 1 |
| fraction bar | — |
| denominator | 6 |
Unit Fractions – Multiplication
Multiples of unit fractions are fractions created by multiplying the fraction by whole numbers. Here is an example:
When multiplying fractions with whole numbers, you need to remember that whole numbers are just fractions with the denominator 1, since they are wholes. In the example above we multiply the whole number 2 by $\frac{1}{3}$. so the operation looks like this:
- 2 x $\frac{1}{3}$
Knowing that the whole number 2 can be displayed as $\frac{2}{1}$, the operation can also look like this:
- $\frac{2}{1}$ x $\frac{1}{3}$ = $\frac{2}{3}$
If you multiply the numerator and the denominator, you solve for 2 x 1 = 1 and 1 x 3 = 3 which results in the fraction $\frac{2}{3}$.
Unit Fractions – Follow-Up Activities
After the video there is continued practice with learning about how to multiply a unit fraction by an integer. Have a go at one of the unit fractions worksheet activities after watching the video.
Transcript Fractions as a Multiple of Unit Fractions
Axel and Tank are going to dinner at their favourite pizza restaurant. They need to work out which pizza has enough slices to make a whole pizza for them to share. We can help Axel and Tank work out how much of each pizza there is by multiplying unit fractions by an integer. A unit fraction is a fraction that has one as the numerator and a whole number as the denominator. One-sixth is an example of a unit fraction. The whole is divided into six equal parts and each part has a value of one-sixth. We can use repeated addition to find multiples of unit fractions or look at them as multiples on a number line. We can also multiply the unit fraction by a whole number, or integer, by setting up a multiplication equation. Let’s look at the anchovy pizzas in the case. The anchovy pizzas are divided into thirds and each slice has a value of one-third. Now, look at the number of pizza slices. There are two, ‘one-third’ slices. We can write this as a multiplication equation to calculate the total amount of anchovy pizza available. First, write the number of unit fractions being grouped. There are two. Next, write the unit fraction that is represented. The unit fraction is one-third. We are going to multiply two times one-third. First, let's look at the denominator. The whole is still divided into thirds, so the denominator in the answer doesn’t change. Now, multiply the whole number, the integer, with the numerator, two times one is two. The anchovy pizza has two-thirds of a pizza available, which is not enough for Axel and Tank to share a whole pizza. "Sigh!" Next let's work out how much of the veggie delight pizza is available. First, look at the number of unit fractions being grouped and the unit fraction. How many slices, or unit fractions, of pizza are being grouped? There are four. What is the unit fraction for the veggie pizza? As there are five parts, or slices, in a whole pizza the unit fraction is one-fifth. The next step is to write a multiplication equation. What are we multiplying? Four times one-fifth. When we multiply, the denominator remains the same because the pizza is still cut into fifths. Multiply the integer or whole number by the numerator, four times one is four. There are four-fifths of a veggie delight pizza in the case which is still not enough to make a whole pizza to share. Finally, let's calculate how much of the under the sea supreme pizza is available. What is the first step? Count how many unit fractions there are. There are six. What is the second step? Determine the unit fraction for the number of parts the whole pizza is divided into. What is the unit fraction for the under the sea supreme? The unit fraction is one quarter. What is the next step? Set up the multiplication equation. What are we multiplying? Six times one quarter. How much of the pizza is in the case? There are six quarters of under the sea supreme pizza. Six quarters or one and a half. There is more than enough for the very hungry Axel and Tank to order a whole pizza! Remember, we can find the multiples of a unit fraction through multiplication. First, find the number of unit fractions being grouped together and then, write the unit fraction being represented. Multiply the whole number and the unit fraction. When multiplying, start with the denominator. The denominator doesn't change. Finally, multiply the whole number with the numerator. “Mmmmm, under the sea supreme!” “My favourite!”
Fractions as a Multiple of Unit Fractions exercise
-
Help Axel and Tank to choose a whole pizza.
HintsIf the numerator and denominator are the same, this is equivalent to a whole. $\frac2 6$ + $\frac4 6$ = $\frac6 6$ which is 1 whole.
Count all the slices of pizza. Is this the same as the number of portions it has been cut into?
Solution- The first pizza has $\frac3 4$ in total. This is NOT equivalent to a whole.
- The second pizza has $\frac3 3$ in total. This IS equivalent to a whole, so is CORRECT.
- The third pizza has $\frac5 6$ in total. This is NOT equivalent to a whole.
- The fourth pizza has $\frac8 8$ in total. This IS equivalent to a whole, so is CORRECT.
-
Multiplying pizza slices.
HintsCount how many pizza slices there are in total. This is the factor you are multiplying by.
Count how many parts the pizza has been sliced into. If it has been sliced into 6, the unit fraction would be $\frac1 6$.
Solution- For the first pair: There are 5 slices in total and each slice is $\mathbf{\frac{1}{4}}$, since the pizzas have been cut into 4 parts.
- For the second pair: There are 5 slices in total and each slice is $\mathbf{\frac{1}{6}}$, since the pizzas have been cut into 6 parts.
- For the third pair: There are 5 slices in total and each slice is $\mathbf{\frac{1}{3}}$, since the pizzas have been cut into 3 parts.
- For the fourth pair: There are 4 slices in total and each slice is $\mathbf{\frac{1}{5}}$, since the pizzas have been cut into 5 parts.
-
Cookie dough dessert.
HintsHow many slices do they eat in total?
Have they eaten more than a whole cookie dough pizza?
If they have eaten a whole cookie dough pizza plus a bit more, then the answer should be a mixed number.
SolutionAxel and Tank eat 7 slices. Each slice is $\mathbf{\frac{1}{6}}$ so we need to find: 7 x $\mathbf{\frac{1}{6}}$.
Since $\mathbf{\frac{6}{6}}$ is equal to one whole, we know that they have eaten 1 whole pizza PLUS $\mathbf{\frac{1}{6}}$ of a pizza which equals: 1$\mathbf{\frac{1}{6}}$
-
Multiply the unit fractions.
HintsFirst, multiply the factor by the numerator. For example, with 5 x $\frac1 3$ solve 5 x 1. Then write this above the denominator. $\frac5 3$.
Convert the improper fraction into a mixed number: $\frac5 3$ becomes 1 $\frac2 3$.
Solution- Axel and Tank are ordering lots of pizzas for a pizza party. They order 10 x $\mathbf{\frac{1}{3}}$ veggie slices of pizza. In total they have 3 $\mathbf{\frac{1}{3}}$ veggie pizzas.
- They order 8 x $\mathbf{\frac{1}{5}}$ anchovy slices of pizza. In total they have 1 $\mathbf{\frac{3}{5}}$ anchovy pizzas.
- Finally, they order 9 x $\mathbf{\frac{1}{4}}$ sea supreme slices of pizza. In total they have 2 $\mathbf{\frac{1}{4}}$ sea supreme pizzas.
-
What is a unit fraction?
HintsCount how many parts the pizza shape has been cut into. This is the bottom part of your fraction (the denominator). For example, a pizza cut into 5 parts, would have 5 as the denominator.
Remember that a unit fraction always has 1 as the numerator (top part of the fraction).
SolutionThis pizza shape has been cut into three parts, so the bottom part of the fraction (denominator) is 3.
Each slice is 1 out of 3 or $\frac1 3$. A unit fraction always has 1 as the numerator.
-
Ordering fractions.
HintsIf the answer can be simplified, reduce it to its simplest form.
Convert the improper fraction to a mixed number.
First, multiply the factor by the numerator to find the improper fraction.
SolutionThe order of the totals from smallest to largest are:
- 10 x $\mathbf{\frac{1}{8}}$ = 1$\frac2 8$ = 1 $\mathbf{\frac{1}{4}}$
- 6 x $\mathbf{\frac{1}{4}}$ = 1$\frac2 4$ = 1 $\mathbf{\frac{1}{2}}$
- 14 x $\mathbf{\frac{1}{8}}$ = 1$\frac6 8$ = 1$\mathbf{\frac{3}{4}}$
- 9 x $\mathbf{\frac{1}{4}}$ = 2$\mathbf{\frac{1}{4}}$
- 5 x $\mathbf{\frac{1}{2}}$ = 2$\mathbf{\frac{1}{2}}$

Fractions as a Multiple of Unit Fractions
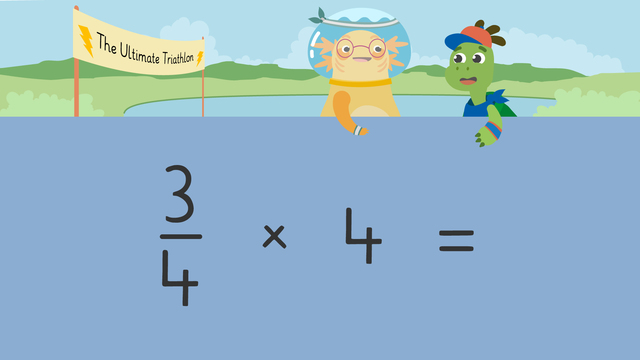
Multiplying a Fraction by a Whole Number

Multiplying Fractions Less Than One
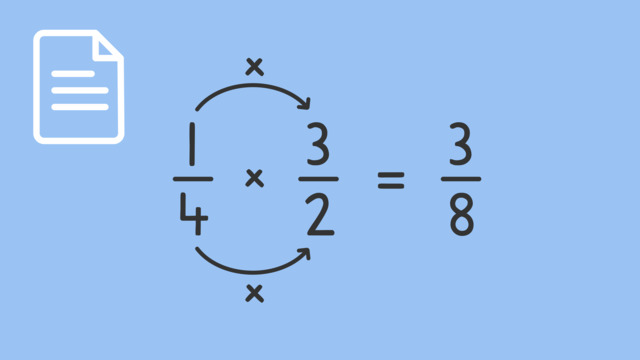
Multiplying Fractions
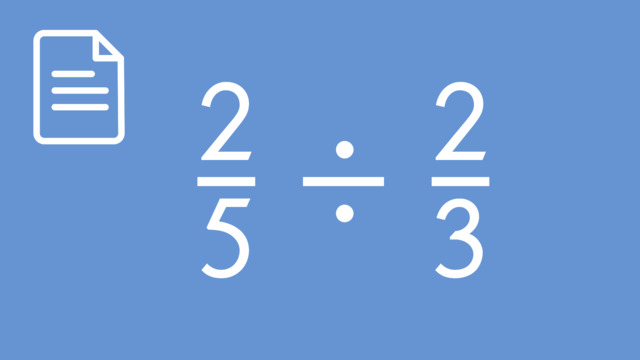
Dividing Fractions
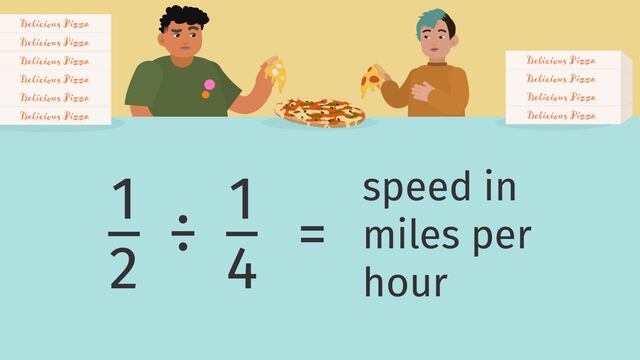
Ratios of Fractions

Dividing Whole Numbers by Unit Fractions Using Models

Lowest Common Multiples

Multiplying Mixed Numbers: Word Problems

Finding the Greatest Common Factor
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?












