Multiplying a Fraction by a Whole Number
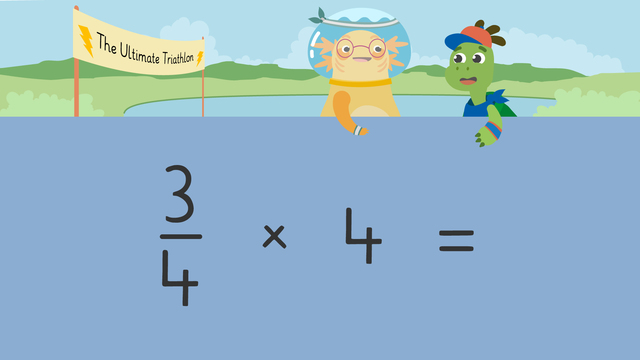

Basics on the topic Multiplying a Fraction by a Whole Number
How to Multiply Fractions with Whole Numbers
Multiplying fractions by whole numbers is a more efficient way to add a group of repeated fractions.This text will show how multiplying a fraction with a whole number works using models and symbols. For continued practice, there is a multiplying fractions by a whole number worksheet available after watching the video. In this next step, let’s look at the necessary steps to multiplying fractions with whole numbers with the help of an example.
Multiplying Fractions with Whole Numbers – Steps
These are the steps to multiplying a whole number by a fraction:
- First, write the fraction.
- Next, write the whole number as a fraction with a denominator of one.
- Multiply the numerators.
- Multiply the denominators.
- Rewrite the fraction as a mixed number if needed.
Multiplying Fractions with Whole Numbers – Example
In This example, we investigate how to multiply $\frac{2}{3}$ by 2.
First of all we write our fraction $\frac{2}{3}$ and then write our whole number as a fraction with a denominator of 1: $\frac{2}{1}$.
We then multiply the numerators.
2 x 2 = 4.
And then the denominators.
3 x 1 = 3.
We then have the fraction $\frac{4}{3}$ which can be rewritten as 1 $\frac{1}{3}$.
Multiplying Fractions with Whole Numbers – Summary
Remember the steps for multiplying fractions with whole numbers? The table below shows you the required steps.
| Step # | What to do |
|---|---|
| 1 | Write the fraction. |
| 2 | Write the whole number as a fraction with a denominator of one. |
| 3 | Multiply the numerators. |
| 4 | Multiply the denominators. |
| 5 | Rewrite the fraction as a mixed number if needed. |
For continued practice, have a go at our multiplying fractions by a whole number worksheet and interactive problems for KS2.
Transcript Multiplying a Fraction by a Whole Number
“So, start training and come on down to participate in the Ultimate Triathlon!” “Tank, are you thinking what I’m thinking?” “That it’s time for dinner?”
“No. Well, yes, but I think we should take part in the triathlon!” Axel and Tank are going to need to spend a portion of time each week on cycling, swimming and running in order to prepare for the triathlon. We can help Axel and Tank get ready for the event by "Multiplying Fractions by Whole Numbers" to keep track of their training routines. Axel and Tank are going to cycle for two-thirds of an hour, twice a week.
We know that we can add fractions to find the total. Two-thirds plus two-thirds equals four-thirds. Although, repeated addition becomes tricky when we have more groups, we can also multiply fractions by whole numbers because it is a more efficient way to solve the problem. To multiply fractions by a whole number, first, start with the fraction that is shown: two-thirds. We are going to multiply that by the number of groups we have, which is two. Next, rewrite the whole number as a fraction. So we need to add a denominator. Since a denominator tells us how many parts a whole is divided into, think about how many parts make up a whole. A whole number is NOT divided into parts, so there is only 1 in the WHOLE, meaning the denominator is ONE. Now, let's multiply two-thirds times two. Multiply the numerators: two times two equals four. Now multiply the denominators: three times one equals three. Two-thirds times two equals four-thirds. Four-thirds is an improper fraction because four is more than three, so it can be rewritten as one and one-third. Axel and Tank will ride their bikes for one and a third hours each week. They will also need to train for the running event. To set up the multiplication equation for this problem, the first step is to write the fraction. What fraction of the hour do they plan on training for? They will train for three-quarters of an hour. How many times a week will they run? They will run four times a week. Our equation is three-quarters times four. The next step is to rewrite four as a fraction by putting a one as the denominator. Now, multiply the numerators: three times four equals twelve, and multiply the denominators: four times one equals four. The answer is twelve-quarters, which can be rewritten as three wholes. Axel and Tank will run for three hours a week. Since swimming is their favorite, they are planning on swimming A LOT! How much time in an hour do they plan to spend on swimming? They are going to swim eight-twelfths of an hour. How many times a week are they going to swim? Nine times a week. How do we set up the equation? Eight-twelfths times nine over one equals. How many hours a week do they train for swimming? Seventy-two twelfths, which can be rewritten as six. Axel and Tank will swim for six hours each week! "Remember, we multiply fractions by whole numbers because it is a more efficient way to solve the problem." First, write the fraction. Next, write the whole number as a fraction with a denominator of one. Multiply the numerators. Multiply the denominators Rewrite the fraction as a mixed number if needed. “TANK, WE DID IT!” “Yes! All that hard work paid off!” “It was a beautiful day today at The Ultimate Triathlon. We are SO proud of all of the contestants.”
Multiplying a Fraction by a Whole Number exercise
-
Which fractions do the shaded shapes represent?
HintsThink about the proportion of the circle that is shaded. For example, this circle is $\frac{3}{4}$ shaded.
Can you simplify the fractions with the larger denominators to help you?
SolutionHere are the fractions that match each shape.
- The first shape represents $\frac{1}{4}$. $\frac{3}{12}$ can be simplified to $\frac{1}{4}$ by dividing both the numerator and the denominator by 3.
- The second shape represents $\frac{1}{3}$. $\frac{2}{6}$ can be simplified to $\frac{1}{3}$ by dividing both the numerator and the denominator by 2.
- The third shape represents $\frac{1}{2}$. $\frac{4}{8}$ can be simplified to $\frac{1}{2}$ by dividing both the numerator and the denominator by 4. $\frac{6}{12}$ can also be simplified to $\frac{1}{2}$ by dividing both the numerator and the denominator by 6.
- The fourth shape represents $\frac{2}{3}$. $\frac{4}{6}$ can be simplified to $\frac{2}{3}$ by dividing both the numerator and the denominator by 2. $\frac{6}{9}$ can also be simplified to $\frac{2}{3}$ by dividing both the numerator and the denominator by 3.
-
Can you help Axel and Tank?
HintsStart by finding the fraction you are multiplying.
We can write the whole number as a fraction to help us find the answer.
Are there any words in the text that could help you with ordering?
SolutionThese are the correctly ordered steps that Axel and Tank should follow:
- First, write the fraction.
- Write the whole number as a fraction.
- Multiply the numerators.
- Multiply the denominators.
- Finally, re-write the fraction as a mixed number if necessary.
-
Find the times for each exercise.
HintsUse the shaded circle to help you e.g. this circle represents $\frac{3}{4}$.
Remember, you can make the whole number into a fraction like this to help you with the multiplication.
You could get some paper and a pen to help you if you need to.
SolutionThis is how long Axel and Tank will do each exercise each week.
- Cycling = $\frac{3}{6}$ x 5 = $\frac{3}{6}$ x $\frac{5}{1}$ = $\frac{15}{6}$ = 2 $\frac{3}{6}$ = 2 $\mathbf{\frac{1}{2}}$
- Running = $\frac{7}{8}$ x 3 = $\frac{7}{8}$ x $\frac{3}{1}$ = $\frac{21}{8}$ = 2 $\mathbf{\frac{5}{8}}$
- Swimming = $\frac{9}{10}$ x 7 = $\frac{9}{10}$ x $\frac{7}{1}$ = $\frac{63}{10}$ = 6 $\mathbf{\frac{3}{10}}$
- Walking = $\frac{1}{3}$ x 6 = $\frac{1}{3}$ x $\frac{6}{1}$ = $\frac{6}{3}$ = 2
-
Solve the multiplication problems
HintsHow can you change the whole number to make it easier to multiply?
Remember to re-write your final fraction at the end as a mixed number if necessary.
SolutionAxel and Tank have spent this many hours doing these activities.
- Watching TV= $\frac{4}{5}$ x 6 = $\frac{4}{5}$ x $\frac{6}{1}$ = $\frac{24}{5}$ = 4 $\mathbf{\frac{4}{5}}$
- Cooking = $\frac{3}{4}$ x 8 = $\frac{3}{4}$ x $\frac{8}{1}$ = $\frac{24}{4}$ = 6
- Cleaning = $\frac{4}{7}$ x 3 = $\frac{4}{7}$ x $\frac{3}{1}$ = $\frac{12}{7}$ = 1 $\mathbf{\frac{5}{7}}$
- Reading = $\frac{6}{9}$ x 4 = $\frac{6}{9}$ x $\frac{4}{1}$ = $\frac{24}{9}$ = 2 $\frac{6}{9}$ = 2 $\mathbf{\frac{2}{3}}$
-
Can you work out how long Axel and Tank want to cycle for now?
HintsYou are trying to solve $\frac{2}{3}$ x 3.
When multiplying a fraction by a whole number, what can we do to the whole number to make it easier to solve?
Can you simplify the fraction you are left with?
SolutionHere is the completed expression:
- We can change 3 into $\frac{3}{1}$
- $\frac{2}{3}$ x $\frac{3}{1}$ = $\frac{6}{3}$
- $\frac{6}{3}$ can be simplified to 2.
- The correct answer is 2 hours.
-
Can you check the multiplication equations?
HintsWhen we make the whole number into a fraction, the denominator is always...?
Have the answers been simplified correctly?
SolutionThese are the parts that should have been highlighted.
The equations written correctly are:
- $\frac{6}{7}$ x 5 = $\frac{6}{7}$ x $\mathbf{\frac{5}{1}}$ = $\frac{30}{7}$ = 4 $\frac{2}{7}$
- $\frac{5}{8}$ x 9 = $\frac{5}{8}$ x $\frac{9}{1}$ = $\mathbf{\frac{45}{8}}$ = 5 $\frac{5}{8}$
- $\frac{4}{6}$ x 8 = $\frac{4}{6}$ x $\frac{8}{1}$ = $\frac{32}{6}$ = 5
- $\frac{6}{12}$ x 3 = $\frac{6}{12}$ x $\frac{3}{1}$ = $\mathbf{\frac{18}{12}}$ = 1 $\frac{1}{2}$

Fractions as a Multiple of Unit Fractions
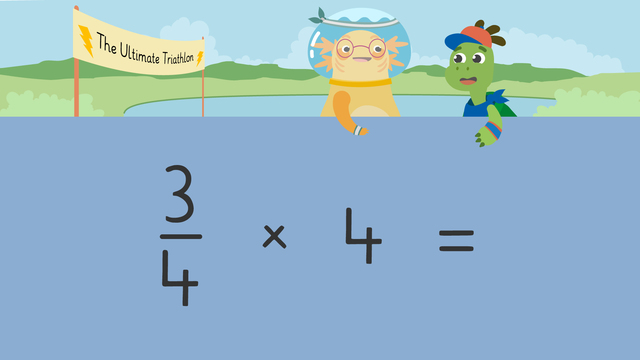
Multiplying a Fraction by a Whole Number

Multiplying Fractions Less Than One
Multiplying Fractions
Dividing Fractions
Ratios of Fractions

Dividing Whole Numbers by Unit Fractions Using Models

Lowest Common Multiples

Multiplying Mixed Numbers: Word Problems

Finding the Greatest Common Factor
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?











how can axel breathe in a fish tank and also how is he sweating if he has lot of water