Simplifying Fractions
Basics on the topic Simplifying Fractions
Simplifying Fractions
When teaching simplifying fractions, we need to know what a fraction is.
A fraction is a part of a whole. The number of equal pieces that the whole is divided into is called the denominator while the numerator is the number of equal pieces of the whole that we are interested in.
In the fraction above ($\frac{1}{4}$), the whole is divided into 4 pieces. If the whole is divided into 6 equal parts and we are interested in five pieces as shown below, the numerator is 5 and the denominator is 6.
Read on to find out more about simplifying fractions (Year 5) and have a look at a simplifying fractions activity.
Simplifying Fractions – Examples
Let’s have a look at some examples of simplifying fractions (you can see more in our video on simplifying fractions). Sometimes fractions can look different but are actually the same because they represent the same amount. Such fractions are called equivalent fractions. For example the two pictures show two ways of representing one third.
The first picture shows $\frac{2}{6}$ in which 2 out of the 6 equal sections are shaded. The second picture shows $\frac{1}{3}$ in which 1 out of the 3 equal sections are shaded. Notice that in the first picture although 2 out of the 6 equal sections are shaded, the shaded amount of the whole figure remains the same. Therefore the two figures show equivalent fractions.
How to Simplify Fractions by Using Common Factors
Fractions can be simplified to make them easy to understand. Looking at the two figures from earlier, it is easier to understand $\frac{1}{3}$ than $\frac{2}{6}$. Therefore we can simplify $\frac{2}{6}$ to get $\frac{1}{3}$.
To simplify a fraction, we can follow these steps:
| Step # | What to do |
|---|---|
| 1 | Find a number that both the numerator and denominator are divisible by. |
| 2 | Divide the numerator and denominator by that number. |
| 3 | Repeat steps 1 and 2 until you can no longer divide the numerator and/or the denominator. |
How to Simplify Fractions by Using the Greatest Common Factor
We can simplify a fraction in one step if we divide both numerator and denominator by the largest number that they are both divisible by. This number is called the greatest common factor or GCF.
To find the GCF follow these steps:
| Step # | What to do |
|---|---|
| 1 | List all the factors of the numerator. |
| 2 | List all the factors of the denominator. |
| 3 | The largest number that occurs in both lists is the greatest common factor. |
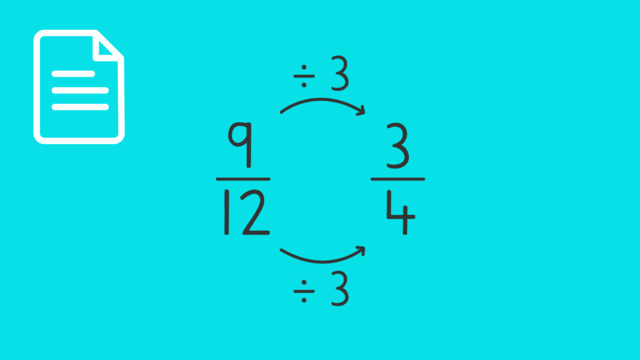
For example, if we are asked to simplify $\frac{10}{12}$ we can do the following:
- Step 1: List the factors of 10 and 12 in order to find the GCF
- Factors of 10 are 1, 2, 5, 10
- Factors of 12 are 1, 2, 3, 4, 6, 12.
- Notice that the largest number in both lists is 2. Therefore, 2 is the GCF.
- Step 2: Divide the numerator and denominator by 2:
- $\frac{10}{12}$ ÷ $\frac{2}{2}$ = $\frac{5}{6}$
We know that this is correct because, from the following diagram, notice that the same portion of the whole is shaded. The only difference is that the whole is divided into different numbers of pieces.
Simplifying Fractions KS2 – Summary
Equivalent fractions are fractions that look different but represent the same amount. To simplify a fraction, divide the numerator and the denominator by the same factor. The best factor to use is the greatest common factor (GCF).
To find the greatest common factor (CGF), you can do the following:
| Step # | What to do |
|---|---|
| 1 | List all the factors of the numerator. |
| 2 | List all the factors of the denominator. |
| 3 | The largest number that occurs in both lists is the greatest common factor. |
Continue learning about simplifying fractions by practicing with our simplifying fractions video, simplifying fractions worksheet and simplifying fractions activities and interactive exercises.
Frequently Asked Simplifying Fractions Questions
Transcript Simplifying Fractions
“Hmmm….I know that sound!” "Mmmmm..." “That’s the sound of my favourite chocolate bar, Succulent Sea Salt!” "BOO!" "AAAGHHHHH!" "Whatcha doin’?" “May I have some, please?” “Sure, if you can solve this riddle.” "Would you rather have twelve-twenty-fourths of the chocolate bar or one-half?" “DEAL!” We can help Tank solve this riddle by “Simplifying Fractions.” Equivalent fractions are fractions that have different numerators and denominators, but are equal to one another because they have the same value. When we simplify fractions, we are making equivalent fractions. We simplify fractions with MANY parts into fractions with FEWER parts to make them easier to understand. Let’s use ten-twelfths as an example. First, we want to think of a common factor that BOTH the numerator and denominator share. What is a common factor of both ten and twelve? Two, since they are both even numbers, two is a factor they share. Next, we divide BOTH the numerator and denominator by two. "Ten divided by two equals five." "Twelve divided by two equals six." The simplified fraction is five-sixths. Is five-sixths equivalent to ten-twelfths? Yes, they have the same value and it’s easier to picture something divided into six parts than something that is divided into twelve parts. Let’s try another example. This fraction is six eighteenths. What is a common factor of both six and eighteen? Since they are both even, we know that they share a common factor of two. Next, we divide both numbers by two. What is six divided by two? Six divided by two equals three. What is eighteen divided by two? Eighteen divided by two is nine. "What is the simplified fraction?" Three-ninths. Three ninths and six eighteenths are equivalent. Take another look at three-ninths. "What do you notice about the numerator, three, and the denominator, nine?" Three and nine both have a common factor of THREE. We can simplify this fraction AGAIN. How do we simplify this fraction? We need to divide the numerator and denominator by three. What is the simplified fraction? The simplified fraction is one third. Let’s compare all of the fractions: Six-eighteenths, three-ninths, and one third are ALL equivalent. One third is the easiest to understand. "Okay, here's Axel's riddle to solve." He was asked if he would rather have twelve-twenty fourths or one half of the chocolate bar. First, we'll take a look at the fraction twelve-twenty-fourths. What do we do first in order to simplify this fraction? Find a common factor of twelve and twenty-four. "Since twelve and twenty-four have several common factors, how do we decide which factor to choose?" If we choose the GREATEST common factor, we will only need to simplify our fraction one time. Let’s list all of the factors of twelve. One, two, three, four, six, twelve. Now list all of the factors of twenty-four. One, two, three, four, six, eight, twelve, twenty-four. What is the greatest common factor that is in both groups? The greatest common factor is twelve. What is the next step? The next step is to divide both the numerator and denominator by twelve. What is the simplified fraction? The simplified fraction is ONE HALF! Let's compare that to the one-half from Axel's riddle, which is a unit fraction and already in its simplest form. The twelve-twenty fourths or one-half of Axel's chocolate bar are THE SAME!
Remember, we simplify fractions with many parts into fewer parts so that they are easier to understand. We simplify a fraction by dividing the numerator and denominator by a common factor that they both share. Sometimes they have more than one common factor, so we can divide the fractions more than once OR choose the GREATEST common factor.
"May I have some, please?"
Simplifying Fractions exercise
-
How much of each chocolate bar has been eaten?
HintsLook for the bars that have the same amount eaten.
How could the numerator and the denominator of the above fraction be divided?
For example, if we divide the numerator and the denominator of $\frac{2}{4}$ by 2, we get $\frac{1}{2}$.
SolutionHere are the matching fractions.
____________
$\frac{2}{6}$ = $\frac{1}{3}$
- If we divide both the numerator and the denominator in $\frac{2}{6}$ by 2, we get $\frac{1}{3}$.
$\frac{4}{8}$ = $\frac{1}{2}$
- If we divide both the numerator and the denominator in $\frac{4}{8}$ by 4, we get $\frac{1}{2}$.
$\frac{2}{10}$ = $\frac{1}{5}$
- If we divide both the numerator and the denominator in $\frac{2}{10}$ by 2, we get $\frac{1}{5}$.
$\frac{3}{12}$ = $\frac{1}{4}$
- If we divide both the numerator and the denominator in $\frac{3}{12}$ by 3, we get $\frac{1}{4}$.
-
How much of each of these bars is white chocolate?
HintsHow many pieces of chocolate are there altogether? How many pieces are white? Write this as a fraction and then simplify it.
For example, this chocolate bar has 10 pieces altogether and 5 of them are white chocolate. That means $\frac{5}{10}$ are made from white chocolate. We could simplify $\frac{5}{10}$ to $\frac{1}{2}$, by dividing both the numerator and the denominator by 5.
Look at the bar and find the fraction that is white.
Solution$\mathbf{\frac{1}{2}}$ of the first bar is made from white chocolate.
- 3 out of 6 squares are white chocolate, therefore $\frac{3}{6}$ is made from white chocolate.
- If we divide the numerator and the denominator by 3 we get $\frac{1}{2}$.
- 2 out of 8 squares are white chocolate, therefore $\frac{2}{8}$ is made from white chocolate.
- If we divide the numerator and the denominator by 2 we get $\frac{1}{4}$.
- 6 out of 9 squares are white chocolate, therefore $\frac{6}{9}$ is made from white chocolate.
- If we divide both the numerator and the denominator by 3 we get $\frac{2}{3}$.
- 10 out of 12 squares are white chocolate, therefore $\frac{10}{12}$ is made from white chocolate.
- If we divide both the numerator and the denominator by 2 we get $\frac{5}{6}$.
-
Can you sort the chocolate bars?
HintsWork out the fraction of caramel chocolate each bar is made from. What can this fraction be simplified to?
For example, this bar is made up of $\frac{6}{8}$ caramel chocolate. If we divide both the numerator and denominator by two we get $\frac{3}{4}$, so we would highlight it in green.
SolutionThese are the bars highlighted correctly.
$\mathbf{\frac{2}{3}}$
- 8 caramel squares and 4 milk squares. There are 12 squares altogether in this bar so $\frac{8}{12}$ is caramel. If we divide the numerator and the denominator by four we get $\frac{2}{3}$.
- 10 caramel squares and 5 milk squares. There are 15 squares altogether in this bar so $\frac{10}{15}$ is caramel. If we divide the numerator and the denominator by five we get $\frac{2}{3}$.
- 9 caramel squares and 3 milk squares. There are 12 squares altogether in this bar so $\frac{9}{12}$ is caramel. If we divide the numerator and the denominator by three we get $\frac{3}{4}$.
- 12 caramel squares and 4 milk squares. There are 16 squares altogether in this bar so $\frac{12}{16}$ is caramel. If we divide the numerator and the denominator by four we get $\frac{3}{4}$.
- 15 caramel squares and 5 milk squares. There are 20 squares altogether in this bar so $\frac{15}{20}$ is caramel. If we divide the numerator and the denominator by five we get $\frac{3}{4}$.
- 4 caramel squares and 6 milk squares. There are 10 squares altogether in this bar so $\frac{4}{10}$ is caramel. If we divide the numerator and the denominator by two we get $\frac{2}{5}$.
- 6 caramel squares and 9 milk squares. There are 15 squares altogether in this bar so $\frac{6}{15}$ is caramel. If we divide the numerator and the denominator by three we get $\frac{2}{5}$.
-
How have these fractions been simplified?
HintsWhat are common factors of the original numerator and denominator?
How many times can the simplified numerator fit into the original numerator?
Solution- $\frac{8}{20}$ are blue. If we divide the numerator and the denominator by 4, we can say that $\frac{2}{5}$ are blue.
- $\frac{12}{15}$ are green. If we divide the numerator and the denominator by 3, we can say that $\frac{4}{5}$ are green.
- $\frac{10}{14}$ are brown. If we divide the numerator and the denominator by 2, we can say that $\frac{5}{7}$ are brown.
- $\frac{15}{25}$ are red. If we divide the numerator and the denominator by 5, we can say that $\frac{3}{5}$ are red.
- $\frac{14}{16}$ are purple. If we divide the numerator and the denominator by 2, we can say that $\frac{7}{8}$ are purple.
-
How much of the bar has Tank munched?
Hints- How many pieces did the bar have at the beginning?
- How many pieces did Tank eat?
- Can you write this as a fraction?
The bar had 6 squares to start with and Tank has eaten 2. Therefore he has eaten $\frac{2}{6}$ of the bar. How could we simplify this fraction?
What are common factors of 2 and 6?
SolutionTank ate $\mathbf{\frac{1}{3}}$ of the bar.
- The bar had 6 pieces.
- Tank ate 2 pieces, so we can say he ate $\frac{2}{6}$ of the bar.
- If we divide both the numerator and the denominator of $\frac{2}{6}$ by 2, we get $\mathbf{\frac{1}{3}}$.
-
Have these fractions been simplified correctly?
HintsWhat are the common factors of the original numerator and denominator?
Use your knowledge of times tables to help you spot mistakes.
SolutionThis is where the highlighter should have gone.
- If we divide the numerator and the denominator in $\frac{16}{24}$ by 8 we get $\frac{2}{3}$, so this one was correct.
- If we divide the numerator and the denominator in $\frac{18}{21}$ by 3 we get $\frac{6}{7}$ not $\frac{5}{7}$, so this one was incorrect.
- If we divide the numerator and the denominator in $\frac{25}{30}$ by 5 we get $\frac{5}{6}$, so this one was correct.
- If we divide the numerator and the denominator in $\frac{6}{18}$ by 6 we get $\frac{1}{3}$ not $\frac{1}{4}$, so this one was incorrect.
- If we divide the numerator and the denominator in $\frac{12}{24}$ by 12 we get $\frac{1}{2}$ not $\frac{1}{3}$, so this one was incorrect.
- If we divide the numerator and the denominator in $\frac{13}{39}$ by 13 we get $\frac{1}{3}$ not $\frac{2}{3}$, so this one was incorrect.


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?