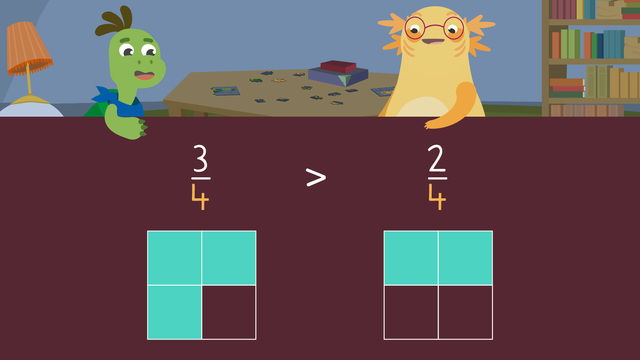
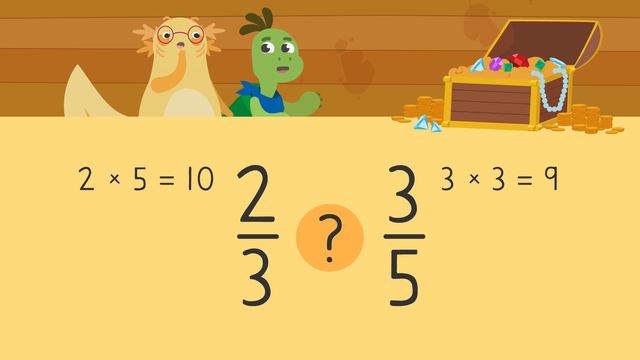Ordering Fractions on a Number Line
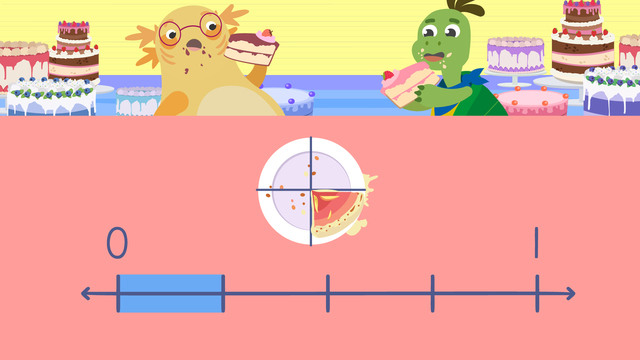

Basics on the topic Ordering Fractions on a Number Line
Axel, Tank, and Dundee just finished a cake eating contest and want to see who won! They need to figure out who has the least amount of cake left by ordering fractions on a number line so they can identify the smallest fraction of cake left!
Transcript Ordering Fractions on a Number Line
"This cake eating contest was fun! I wonder who won?" "It seems like we each have a fraction of cake left. Whoever has the least amount of cake left is the winner." "Oh great! Wait, how do we figure out who won?" Let's help Axel and Tank by ordering fractions on a number line. We can use a number line like this to help us with ordering fractions. For example, Dundee has four-tenths of a cake left, Axel has five-eighths left, and Tank has one-quarter left. Since we are comparing cakes, we will use fraction circles to model the fractions. Here we see four-tenths, five-eighths and one-quarter represented using fraction circles. Now that we've represented the fractions using fraction circles, let's represent them using number lines. Let's start with four-tenths. The denominator tells us that the number line is divided into ten equal parts. That means these lines here represent tenths. Now, count the number of parts from zero shown by the numerator, which is four and label four-tenths here. The next fraction we need to label is five-eighths. The denominator tells us that the number line is divided into eight equal parts. That means these lines here represent eighths. What is the next step? Now, count the number of parts from zero shown by the numerator which is five and label five-eighths here. The last fraction we need to label is one-quarter. What is the first step? Look at the denominator and divide the number line into four equal parts. What is the next step? Now, count the number of parts from zero shown by the numerator which is one and label one-quarter here. Now that we have put each fraction on a number line let's put them together to see which fraction is the smallest? One-quarter is the smallest because it takes up the shortest distance on the number line. Tank has the least amount of cake left, that means he won the cake eating contest! Remember, we can use a number line to help us when ordering fractions. When we label fractions on a number line, first, look at the denominator of each fraction. Next, divide up the number line into equal parts based on the denominator. Finally, count the number of parts from zero shown by the numerator and label the fraction. Repeat these steps until all the fractions are labelled on the number line. "Ughh, maybe I shouldn't have had all those cakes for breakfast." "Dundee! Are you alright!?" "I'm fine! When's dessert?"
Ordering Fractions on a Number Line exercise
-
Can you find the matching pairs?
HintsLook at the coloured sections; they represent the numerator.
The total number of parts in the fraction circle represents the denominator.
The numerator is the number at the top of the fraction, and the denominator is the number at the bottom.
SolutionHere are the matching pairs.
-
How many equal parts should be on the number line?
HintsThe denominator tells us how many equal parts there should be on a number line.
The denominator is the bottom number of a fraction.
The numerator is the top number of the fraction and lets us know how many parts are being counted.
SolutionThis is the correct representation for the fraction $\frac{7}{12}$.
- The denominator is 12 and there are 12 parts altogether.
- The numerator is 7 and there are 7 parts shaded.
-
Determine the fractions and order them.
HintsFirst, work out what fraction is being represented by each number line.
- The total number of parts represents the denominator.
- The green parts represent the numerator.
Once you have labelled each number line with a fraction, you can use the fraction bars to compare which fraction is largest.
Which number line shows the largest fraction? Put the largest fraction next to number 1.
SolutionThe image above shows the fractions in the correct order from largest to smallest.
1) $\frac{3}{4}$
2) $\frac{5}{10}$
3) $\frac{3}{8}$
-
Order the fractions from smallest to largest.
HintsFind the number line that would best represent each fraction.
Remember, the denominator is represented by the total number of parts. You can then shade in the amount of the numerator.
The number line with the fraction plotted closest to zero shows the smallest fraction.
Use this image to help with ordering the first two fractions.
SolutionThe order of the fractions from smallest to largest:
- $\frac{2}{8}$
- $\frac{2}{5}$
- $\frac{2}{3}$
- $\frac{3}{3}$
-
Where do these fractions fall on the number line?
HintsAll of the fractions have the same denominator, so focus on the numerator to place the fraction.
To place the fraction, count the number of parts shown in the numerator from zero.
Place the fraction exactly underneath the counted interval.
Here we can see $\frac{1}{6}$ in the correct spot. Use this to help you fill in the other fractions.
SolutionHere we can see the fractions placed correctly on the number line.
-
Order the fractions from smallest to largest.
HintsUse an extra sheet of paper to make a number line for each fraction.
When fractions have the same numerator, the fraction with the smallest denominator is largest.
When fractions have the same denominator, the fraction with the largest numerator is largest.
SolutionOne example above shows the correct way to solve.
- The judges created 3 number lines and plotted each fraction on a number line.
- After seeing each fraction on a number line, they were able to order them from smallest to largest like this.
- $\frac{2}{8}$, $\frac{1}{3}$, $\frac{3}{5}$ ✔️
- $\frac{4}{10}$, $\frac{4}{8}$, $\frac{4}{5}$ ✔️ is also a correct choice.
$\frac{9}{10}$, $\frac{3}{5}$, $\frac{1}{4}$
- The correct order would be $\frac{1}{4}$, $\frac{3}{5}$, $\frac{9}{10}$
- The correct order would be $\frac{3}{6}$, $\frac{4}{6}$, $\frac{5}{6}$


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?