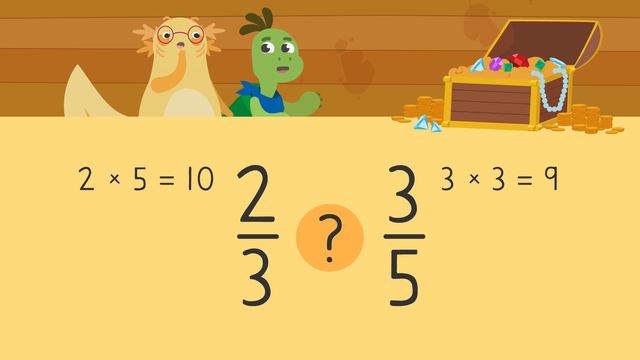Comparing Fractions
Do you want to learn faster and more easily?
Basics on the topic Comparing Fractions
Comparing Fractions
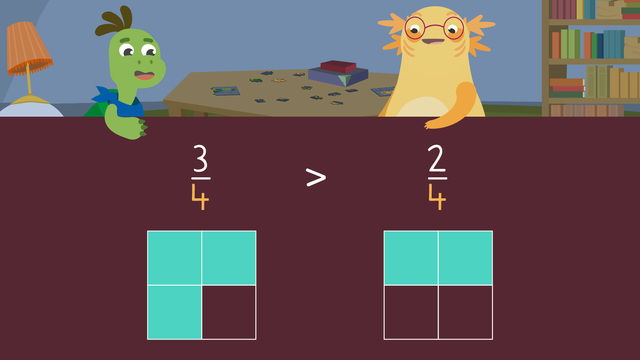
What does comparing fractions mean? Fractions comparing less than 1 means to take two fractions and work out if one is smaller or greater than the other fraction, or if they are both equal! When comparing two fractions, one of the strategies for comparing fractions you can use is comparing fractions with models, such as fraction bars.
Comparing Fractions – Example
Let’s review the process of comparing fractions step by step with an example. In this example we compare $\frac{1}{2}$ and $\frac{1}{2}$. When comparing fractions, you want to do the following:
First, set up a fraction bar for the left side fraction. Since this fraction is one-half, use a one-half fraction bar.
Next, set up a fraction bar for the right side fraction. Since this fraction is one-half, use a one-half fraction bar.
Finally, compare the fraction bars! We can see the two fraction bars are equal, so use the equal to symbol.
If we compare $\frac{1}{2}$ and $\frac{1}{3}$ using a fraction bar, we can see that both fraction bars have just one colored segment but $\frac{1}{3}$ features three segments, whereas $\frac{1}{2}$ just features two. So we conclude that $\frac{1}{2}$ > $\frac{1}{2}$
Comparing Fractions – Summary
When comparing fractions, remember the following steps:
| Step # | What to do |
|---|---|
| 1 | Set up a fraction bar for the left side fraction |
| 2 | Set up a fraction bar for the right side fraction |
| 3 | Compare the fraction bars and use the greater than, equal to, or less than symbol |
This strategy can be used for comparing fractions with the same denominator and comparing fractions with different denominators. After watching the video on how to compare fractions, you will find interactive exercises, worksheets and further activities for comparing fractions in 3rd grade.
Transcript Comparing Fractions
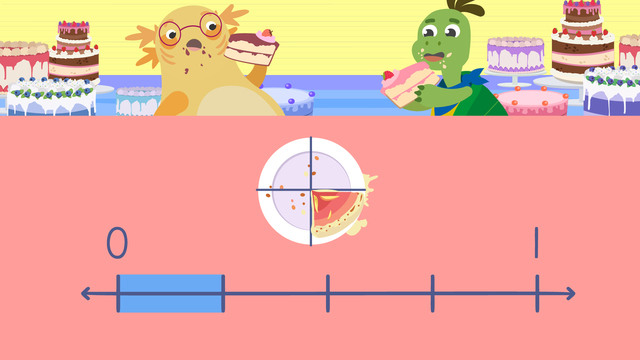
Axel and Tank are excited to sign up for a fun run! "We should do the shorter route!" "Okay, so we need to figure out which one is the shorter distance: two thirds of a mile, or three quarters of a mile?" It looks like Axel and Tank will need help comparing fractions. When comparing fractions we use greater than, less than or equal to symbols. This means the value of the left side is greater than the value on the right side. This means the value of the left side is less than the value on the right side. This means the values on either side are equal. We can use fraction bars to model fractions and compare them. To compare fractions, first, set up a fraction bar for the fraction on the left side. Next, set up a fraction bar for the fraction on the right side. Then, compare the fraction bars. Determine if the fraction on the left is greater than, less than, or equal to the fraction on the right and label using the correct symbol. Let's compare four-eighths and one-quarter! First, set up a fraction bar for four-eighths. The denominator, or bottom number, is eight, so divide the fraction bar into eight equal parts. The numerator, or top number, is four, so shade in four parts of the fraction bar. Now, set up a fraction bar for one-quarter. The denominator is four, so divide the fraction bar into four equal parts. The numerator is one, so shade in one part of the fraction bar. Finally, compare the fractions! We can see four-eighths is bigger than one-quarter, so four-eighths is greater than one-quarter! Now that we have practised comparing fractions, let's help Axel and Tank solve which route is the shortest! The two distances were two thirds of a mile and three quarters of a mile! What is the first step? Create a fraction bar for two thirds. How many equal parts should it have? Three, because the denominator is three. How many parts should we shade in? Two, because the numerator is two. Now let's create a fraction bar for three quarters. How many equal parts are there? Four, because the denominator is four. How many parts should be shaded in? Three, because the numerator is three. What is the next step? Now we compare the fraction bars. Is two thirds greater than, less than or equal to three quarters? Two thirds is less than three quarters so Axel and Tank will run the two thirds of a mile route! Remember, to compare fractions, first, set up a fraction bar for the fraction on the left side. Then, set up a fraction bar for the fraction on the right side. Next, compare the fraction bars. Determine if the fraction on the left side is greater than, less than, or equal to the fraction on the right side and label it using the correct symbol. "I didn't realise it was a colour run Tank, did you?" "No Axel, but it was the best thing ever! Same again next year?" "If we must Tank, just for you."
Comparing Fractions exercise
-
Which symbol makes the following comparison statement correct?
HintsTry using the fraction bars to help compare the fractions.
The symbol should have the open side facing the greater fraction, unless it is equal!
The fractions here are $\frac{1}{3}$ and $\frac{4}{5}$. Since the fraction bar for $\frac{1}{3}$ is smaller than the fraction bar for $\frac{4}{5}$, we use the less than symbol.
$\frac{1}{3}$ < $\frac{4}{5}$.
SolutionLook at the fraction bar for $\frac{2}{3}$.
Then, compare it to the fraction bar for $\frac{3}{4}$.
The fraction bar for $\frac{2}{3}$ is smaller than the fraction bar for $\frac{3}{4}$.
This means we need to use the less than symbol.
The answer is: $\frac{2}{3}$ < $\frac{3}{4}$
-
Match and compare the fraction bars.
HintsThis example fraction bar has five equal parts, with two parts shaded in.
This represents $\frac{2}{5}$.
The phrase for the comparison must compare the fraction bar on the left to the fraction bar on the right.
SolutionThe first fraction bar has 8 equal parts, with 4 parts shaded in. This fraction bar represents $\frac{4}{8}$.
The second fraction bar has 4 equal parts, with 1 part shaded in. This fraction bar represents $\frac{1}{4}$.
Now, compare the fraction bars to help determine the correct symbol to use.
$\frac{4}{8}$ is a bigger fraction than $\frac{1}{4}$.
This means $\frac{4}{8}$ is greater than $\frac{1}{4}$.
-
Can you compare the fractions?
HintsTry using the fraction bars to help compare the fractions.
> means the fraction on the left is greater than the fraction on the right.
< means the fraction on the left is less than the fraction on the right.
= means both fractions are equal.
Solution$\frac{3}{4}$ > $\frac{1}{3}$. Compare the fraction bar for $\frac{3}{4}$ to the fraction bar for $\frac{1}{3}$. $\frac{3}{4}$ is bigger, so use the greater than symbol, >.
$\frac{1}{2}$ = $\frac{2}{4}$. Compare the fraction bar for $\frac{1}{2}$ to the fraction bar for $\frac{2}{4}$. They are both the same size, so use the equal to symbol, =.
$\frac{1}{3}$ < $\frac{2}{4}$. Compare the fraction bar for $\frac{1}{3}$ to the fraction bar for $\frac{2}{4}$. $\frac{1}{3}$ is smaller, so use the less than symbol, <.
$\frac{4}{8}$ = $\frac{3}{6}$. Compare the fraction bar for $\frac{4}{8}$ to the fraction bar for $\frac{3}{6}$. They are both the same size, so use the equal to symbol, =.
-
Which is the correct symbol?
HintsTry using the fraction bars to help compare the fractions.
The symbol should have the open side facing the greater fraction, unless it is equal!
SolutionCompare the fraction bar for $\frac{2}{5}$ to the fraction bar for $\frac{3}{6}$. $\frac{2}{5}$ is smaller, so highlight the less than symbol, <.
Compare the fraction bar for $\frac{4}{5}$ to the fraction bar for $\frac{2}{3}$. $\frac{4}{5}$ is bigger, so highlight the greater than symbol, >.
Compare the fraction bar for $\frac{6}{8}$ to the fraction bar for $\frac{3}{4}$. They are both the same size, so highlight the equal to symbol, =.
-
What do each of the comparison symbols mean?
HintsThink about how you would read this fraction comparison statement from left to right.
Remember, the comparison symbol always opens towards the larger fraction, unless they are the same.
Solution> symbol means greater than.
< symbol means less than.
= symbol means equal to.
-
Can you help Axel and Tank?
HintsDraw equal sized fraction bars to help compare, like this one for $\frac{2}{4}$.
Start by comparing two fractions first. Then compare the third fraction with both of these.
SolutionCreate equal sized fraction bars for all of the distances to compare them.
$\frac{7}{8}$ is greater than $\frac{4}{5}$, $\frac{2}{4}$, and $\frac{1}{3}$, so it goes first.
$\frac{4}{5}$ is greater than $\frac{2}{4}$, and $\frac{1}{3}$, so it goes second.
$\frac{2}{4}$ is greater than $\frac{1}{3}$, so it goes third.
$\frac{1}{3}$ is the smallest fraction, so it goes fourth.
