Fractions with the Same Numerator
Basics on the topic Fractions with the Same Numerator
Comparing Fractions with the Same Numerator
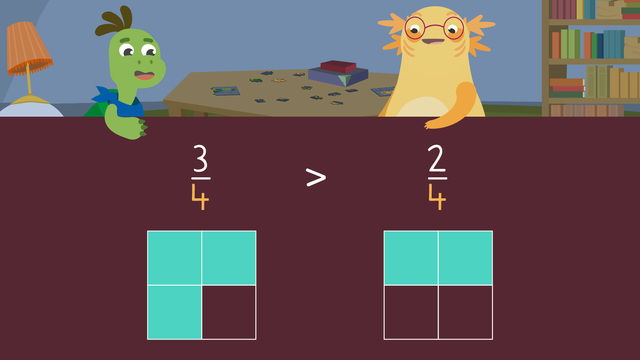
Fractions with the same numerator have the same number of shaded parts, but may have different denominators. As such, we can do comparisons of fractions with the same numerator. When the whole is the same, a smaller number in the denominator means the pieces will be larger since there is less to divide between.
Comparing Fractions with the Same Numerator – Example
Let’s explore how to compare fractions with the same numerator. We can use fraction bars to compare the values of fractions with the same numerator. Let's use the fractions one-half and one-third as examples. Both fractions come from an equal-sized whole. They also both have the same numerator: one. However, their denominators are different.




Comparing Fractions with the Same Numerator – Summary of Steps
How Can I Compare Two Fractions with the Same Numerator? To compare the size of two fractions with the same whole and the same numerator, you need to follow the steps listed in the chart below.
| Step # | What to do |
|---|---|
| 1 | Draw and shade a fraction bar to represent the first fraction. |
| 2 | Draw and shade a fraction bar of identical size to represent the second fraction. |
| 3 | Compare the shaded parts of both bars. |
| 4 | If two fractions with the same whole have the same numerator, but different denominators, the fraction with the smaller denominator is actually larger. |
Comparing Fractions with the Same Numerator – Worksheets
Have you practised yet? After watching the video, you can also find comparing fractions with the same numerator worksheets and exercises.
Transcript Fractions with the Same Numerator
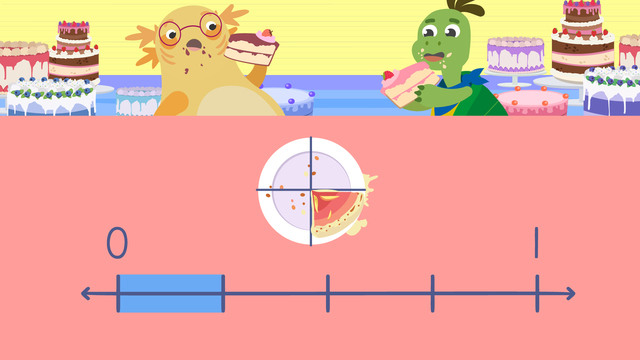
Axel and Tank are training Tank’s new dogfish, Sparky. Using the same-sized treats, they each break it into equal parts and feed him the same number of parts, but Sparky always goes to Axel instead of Tank! They think they are feeding Sparky the same amount, but they will need to learn about "Fractions with the Same Numerator" to work out what is going on! Fractions with the same numerator have the same number of shaded parts but may have different denominators, so we need to compare them closely. When the whole is the same, a smaller denominator means the pieces will be larger since there is less to divide between. To prove this, we can use fraction bars to compare values. Let's use the fractions One half and one third as examples. The whole for both is the same size. They both have the same numerator: one. However, their denominators are different. To compare, draw a fraction bar to represent the first fraction. Next, shade the bar to represent one-half. Then, draw a fraction bar of identical size to represent the second fraction. Now, shade the bar to represent one-third. Finally, compare the shaded parts of both models. One-half has a denominator that is smaller than one-third, but the whole is only divided into two parts so the pieces are actually larger. When comparing fractions with the same numerator and whole, the one with the smaller denominator is actually larger. Let's try this again using Axel and Tank's dogfish treats. Axel has two-quarters of a treat for Sparky, Tank has two sixths. Let's compare by drawing a fraction bar to represent Axel's fraction. Next, shade the bar to show two-quarters. Then, draw a fraction bar of identical size to represent Tank's fraction. Now, shade the bar to show two-sixths. Finally, compare the shaded parts of both bars. Two-quarters has a denominator that is smaller than two-sixths, but the whole is only divided into four parts so the pieces are actually larger. Again, when comparing fractions with the same numerator and whole, the one with the smaller denominator is actually larger so Sparky swims to Axel! Let's try it once more! This time Axel has three-thirds of a treat for Sparky. Tank has three-fifths. Pause the video and predict who has the larger fraction to give Sparky. Let's check our work! First, draw and shade a fraction bar to represent Axel's fraction, three-thirds. Then, draw and shade a fraction bar to represent Tank's fraction, three-fifths. Finally, compare the shaded parts of both models. The shaded value of three-thirds is greater than three-fifths, so Sparky swims to Axel again! Now we know why Sparky always swims to Axel instead of Tank! Before they finish training for the day, let's remember: To compare the size of two fractions with the same whole and the same numerator, first, draw and shade a fraction bar to represent the first fraction. Then, draw and shade a fraction bar of identical size to represent the second fraction. Finally, compare the shaded parts of both bars. If two fractions with the same whole have the same numerator but different denominators, the fraction with the smaller denominator is actually larger. "I'm making certain that Sparky swims to me this time!"
Fractions with the Same Numerator exercise
-
Which fraction is bigger?
HintsLook at the image of Axel and Tank's fish treat. Who has the smaller pieces?
This treat has been broken into six pieces, the denominator is 6. Is each piece of the treat that is $\frac1 6$, larger or smaller than the pieces that are in thirds?
The top number in a fraction is the numerator and the bottom number is the denominator.
SolutionWhen the whole is the same, a smaller number in the denominator means the fraction will be larger.
For example, even though both $\frac1 2$ and $\frac1 3$ have the same numerator, the smaller fraction is $\mathbf{\frac{1}{3}}$.
This is because the larger the denominator, the smaller the fraction.
-
Treats for Sparky.
HintsLook at the denominators. Does the larger fraction have a bigger or a smaller denominator when the numerators are the same?
Look at the size of these fish treats and the size of the denominator. What do you notice?
Try drawing fraction bars of identical size to compare the fractions.
SolutionThe biggest piece will be from the food that is cut into the fewest pieces. Therefore the pieces that have been cut into three parts, where each one is $\mathbf{\frac{1}{3}}$, will be the largest.
-
Comparing fractions of sandwiches.
HintsLook at how many parts the sandwich has been cut into - this is the denominator. The larger the denominator, the smaller the piece.
Look at these two sandwiches. One has been cut into thirds, one has been cut into fifths. Compare a piece of each sandwich. Which would be larger?
SolutionThe order of the parts of the sandwiches from largest denominator to smallest:
- The sandwich cut into eight parts: $\mathbf{\frac{1}{8}}$
- The sandwich cut into six parts: $\mathbf{\frac{1}{6}}$
- The sandwich cut into four parts: $\mathbf{\frac{1}{4}}$
- The sandwich cut into three parts: $\mathbf{\frac{1}{3}}$
-
Compare the fractions with the same numerator.
HintsLook at the denominator. What does a larger denominator mean when the numerators are the same?
When the numerators are the same, the larger the denominator, the smaller the part.
Begin by finding the smallest fraction for Monday. This will be the fraction with the largest denominator.
On Friday Sparky gets the most food, so this will be the fraction with the smallest denominator.
SolutionThese are the correct pairs:
Monday = $\frac3 9$
Tuesday = $\frac3 7$
Wednesday = $\frac3 5$
Thursday = $\frac3 4$
Friday = $\frac3 3$
Each day Sparky always gets three parts (the numerator), since the numerator is the same each time, we only need to compare the denominators.
The larger the denominator, the smaller the fraction. So we order the pieces from Monday to Friday, with the fraction that has the largest denominator first, and the fraction with the smallest denominator last, as this piece will be the biggest.
-
Help Sparky choose the bigger piece.
HintsLook at the denominator. When the numerators are the same, the larger the denominator, the smaller the fraction.
In these two fractions: $\frac1 3$ and $\frac1 2$, which is the bigger fraction? Look at its denominator.
Solution$\frac1 4$ is larger than $\frac1 6$. The symbol to show this is $\frac1 4$ > $\frac1 6$. When both pieces of food are broken up, the one that is broken into more pieces, means that each piece ends up smaller.
-
Compare the fractions.
HintsTry drawing fraction bars to compare the two fractions.
Remember that when the numerators are the same, we only need to look at the denominators to compare the fractions.
When the numerators are the same, the larger the denominator, the smaller the fraction.
Solution- $\frac2 8$ < $\frac2 3$
- $\frac4 9$ < $\frac4 6$
- $\frac2 8$ > $\mathbf{\frac{2}{9}}$
- $\frac{4}{11}$ > $\frac{4}{12}$
- $\frac{7}{10}$ > $\mathbf{\frac{7}{12}}$
- $\frac8 9$ < $\frac8 5$


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?