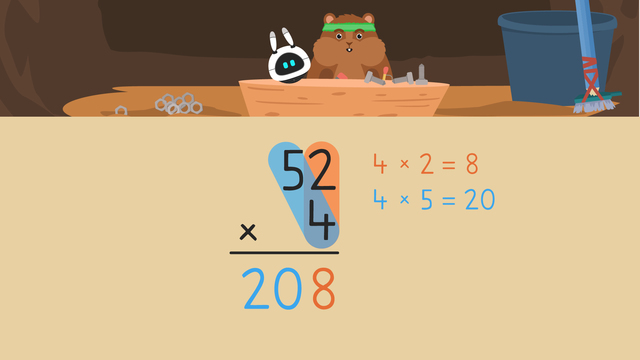Distributive Property of Multiplication — Let's Practise!


Basics on the topic Distributive Property of Multiplication — Let's Practise!
Today we are practising distributive property of multiplication with Razzi! This video contains examples to help you further practise and grow confident in this topic.
Transcript Distributive Property of Multiplication — Let's Practise!
Razzi says get these items ready because today we're going to practise the distributive property of multiplication. It's time to begin! Solve twelve times five by breaking down the twelve and distributing the five. Pause the video to work on the problem and press play when you are ready to see the solution! Break the twelve down into ten and two. Distribute the five. Ten times five is fifty. Two times five is ten. Fifty plus ten equals sixty. Did you also get sixty? Let's tackle the next problem! Solve three times fifteen by distributing the three and breaking down the fifteen. Pause the video to work on the problem and press play when you are ready to see the solution! Break down the fifteen into ten and five. Distribute the three. Three times ten is thirty. Three times five is fifteen. Thirty plus fifteen equals forty-five. Did you also get forty-five? Let's tackle the final problem! Solve eight times nine by distributing the eight and breaking down the nine. Pause the video to work on the problem and press play when you are ready to see the solution! Break down the nine into five and four. Distribute the eight. Eight times five is forty. Eight times four is thirty-two. Forty plus thirty-two equals seventy-two. Did you also get seventy-two? Razzi had so much fun practising with you today! See you next time!
Distributive Property of Multiplication — Let's Practise! exercise
-
Solve 6 $\times$ 15.
HintsBreak down the larger number into 2 smaller numbers that add to equal this larger number.
For example: 7 $\times$ 14 is equivalent to 7 $\times$ (10 + 4)
Next, distribute the number on the outside of the brackets with the numbers on the inside.
For example: for 7 $\times$ (10 + 4), we would multiply 7 $\times$ 10 and 7 $\times$ 4 separately.
Finally, you add the two products you calculated in the previous step.
For example: 7 $\times$ 10 = 70, and 7 $\times$ 4 = 28. So, you add 70 and 28 to get 98. The answer is 98.
Solution6 $\times$ 15 is equivalent to 6 $\times$ (10 + 5)
We distribute the 6 to the numbers inside the brackets:
6 $\times$ 10 = 60 and 6 $\times$ 5 = 30
We add the 60 and the 30 and get 90.
-
Use the distributive property to write equivalent expressions.
HintsBreak down the larger number into 2 smaller numbers that add to equal this larger number. These smaller numbers are called addends.
For example: in the expression 7 $\times$ (10 + 4), 10 and 4 are addends.
If the larger number is between 11 and 19, one of its addends should be 10. There are often multiple possible addends to use, but writing one of them as 10 is usually the easiest way to solve.
Solution7 $\times$ 14 is equivalent to 7 $\times$ (10 + 4) because 14 = 10 + 4
18 $\times$ 3 is equivalent to (10 + 8) $\times$ 3 because 18 = 10 + 8
7 $\times$ 8 is equivalent to 7 $\times$ (4 + 4) because 8 = 4 + 4
17 $\times$ 6 is equivalent to (10 + 7) $\times$ 6 because 17 = 10 + 7
-
Solve the multiplication problem.
HintsIn order to determine how many guests Ethan has room to invite to the party, we need to determine how many total chairs there will be around the tables.
To do this, multiply the number of tables by the number of chairs each table fits.
There are 3 tables, and each table fits 14 chairs. Therefore, we need to multiply 3 by 14.
Break down the 14 into two numbers that add to equal 14.
(Setting one of these numbers as 10 is easiest for the calculation later).
Then, distribute the 3 with these two numbers. This means multiply the 3 by these numbers.
Finally, add the two products.
3 $\times$ 10 = 30
3 $\times$ 4 = 12
30 + 12 = ?
SolutionThe correct answer is 42.
In order to determine how many guests Ethan has room to invite to the party, we need to determine how many total chairs there will be around the tables. To do this, multiply the number of tables by the number of chairs each table fits. There are 3 tables, and each table fits 14 chairs. Therefore, we need to multiply 3 by 14.
3 $\times$ 14 is equivalent to 3 $\times$ (10 + 4)
We distribute the 3 to the numbers inside the brackets:
3 $\times$ 10 = 30 and 3 $\times$ 4 = 12
Finally, we add the 30 and the 12 and calculate 42 guests.
-
Solve the multiplication problem.
HintsIn order to determine how much money Sara will spend on party bags, we need to multiply the cost of each party bag by the number of guests.
Each party bag costs £4, and there will be 13 guests. Therefore, we need to multiply 4 by 13.
Break down the 13 into two numbers that add to equal 13.
(Setting one of these numbers as 10 is easiest for the calculation later).
Then, distribute the 4 with these two numbers. This means multiply the 4 by these numbers.
Finally, add the two products.
4 $\times$ 10 = 40
4 $\times$ 3 = 12
40 + 12 = ?
SolutionThe correct answer is £52.
In order to determine how much money Sara will spend on party bags, we need to multiply the cost of each party bag by the number of guests.
Each party bag costs £4, and there will be 13 guests. Therefore, we need to multiply 4 by 13.
4 $\times$ 13 is equivalent to 4 $\times$ (10 + 3)
We distribute the 4 to the numbers inside the brackets:
4 $\times$ 10 = 40 and 4 $\times$ 3 = 12
Finally, we add the 40 and the 12 and calculate 52 pounds.
-
Solve 8 $\times$ 11.
HintsWe can break down the 11 into 10 + 1.
If we break down the 11 into 10 + 1...
8 $\times$ 11 would be equivalent to 8 $\times$ (10 + 1).
8 $\times$ 10 = 80
8 $\times$ 1 = 8
88 + 8 = ?
SolutionThe correct answer is 88.
11 can be partitioned into 10 + 1.
We can then multiply 8 $\times$ 10 and 8 $\times$ 1.
- 8 $\times$ 10 = 80
- 8 $\times$ 1 = 8
- 80 + 8 = 88
-
Use the distributive property to calculate the following products.
HintsBreak down the larger number into two smaller numbers to write an equivalent expression.
For example: 11 $\times$ 9 is equivalent to (10 + 1) $\times$ 9
Distribute the number on the outside of the brackets.
For example: (10 + 1) $\times$ 9 = 10 $\times$ 9 + 1 $\times$ 9
Add the two products.
For example: 10 $\times$ 9 + 1 $\times$ 9 = 90 + 9 = ?
SolutionBreak down the larger number into two smaller numbers to write an equivalent expression:
11 $\times$ 9 is equivalent to (10 + 1) $\times$ 9
Then, distribute the number on the outside of the brackets:
(10 + 1) $\times$ 9 = 10 $\times$ 9 + 1 $\times$ 9
Finally, add the two products:
90 + 9 = 99
4 $\times$ 12 = 4 $\times$ (10 + 2) = 4 $\times$ 10 + 4 $\times$ 2 = 40 + 8 = 48
5 $\times$ 20 = 5 $\times$ (10 + 10) = 5 $\times$ 10 + 5 $\times$ 10 = 50 + 50 = 100
2 $\times$ 13 = 2 $\times$ (10 + 3) = 2 $\times$ 10 + 2 $\times$ 3 = 20 + 6 = 26


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?