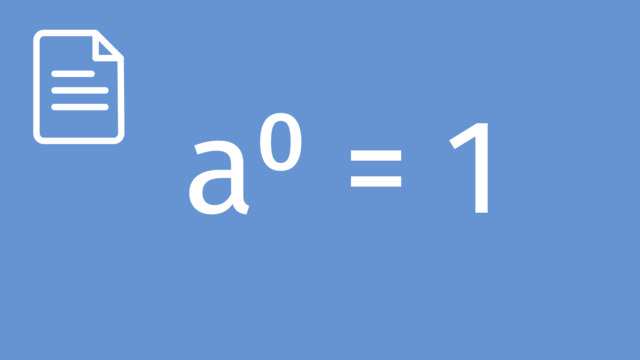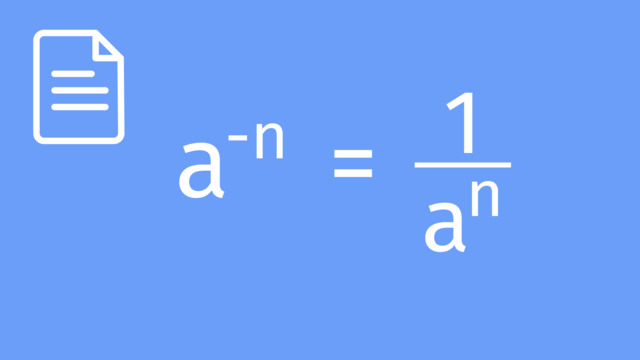Multiplying Indices
Learning text on the topic Multiplying Indices
Multiplying Indices
Indices are more than just numbers on paper; they're a key part of the maths you'll encounter in and out of school. Think of indices as a shortcut for repeated multiplication, simplifying how we handle larger numbers. In everyday life, you see them in situations like calculating how fast a popular video goes viral or understanding how interest on your savings account works. This guide will dive into multiplying powers with the same base, showing you why the rule "keep the base and add the indices" makes sense through expansion.
Understanding Multiplying Indices
To grasp why we add indices, also called exponents or powers, when multiplying powers of the same base, it's helpful to look at the process of expansion.
When multiplying powers with the same base, keep the base the same and find the sum of the exponents, or indices.
Let's use some simple numbers for clarity. Consider $2^3 \cdot 2^2$ ($\cdot$ can be used instead of $\times$ as a multiplication symbol). Here, $2$ is the base, and $3$ and $2$ are the exponents. We can expand these terms to understand the addition of exponents:
- $2^3$ means multiplying $2$ by itself $3$ times, which is $2 \cdot 2 \cdot 2$.
- $2^2$ means multiplying $2$ by itself $2$ times, which is $2 \cdot 2$.
When you multiply $2^3$ and $2^2$, you're essentially multiplying $2$ by itself $3 + 2=5$ times. Therefore, $2^3 \cdot 2^2 = 2^{(3+2)} = 2^5$.
If you are finding it hard to follow the text, we recommend consolidating your understanding of powers by watching this video: Understanding Powers of 10.
See how much you understand about multiplying exponents so far with this interactive quiz!
Multiplying Indices – Example
Let’s see how the above explanation looks in practice. In the following table, you will see step by step progression from a multiplication equation, to expansion, to the addition of the indices and finally simplification:
| Multiply | Expansion | Add the Indices | Simplify |
|---|---|---|---|
| $6^3 \cdot 6^5$ | $6 \cdot 6 \cdot 6) \cdot (6 \cdot 6 \cdot 6 \cdot 6 \cdot 6)$ | $6^{(3+5)}$ | $6^8$ |
| $n^2 \cdot n^4$ | $(n \cdot n) \cdot (n \cdot n \cdot n \cdot n)$ | $n^{(2+4)}$ | $n^6$ |
The process of multiplying indices can be used in some real-world problems, such as multiplying and dividing numbers in scientific notation, or standard form, which is helpful when working with very large or very small numbers.
Multiplying Indices – Application
Tips for Multiplying Indices:
- Understand the Base: Remember that the base number remains the same when multiplying indices.
- Expand for Clarity: Breaking down the expression by expanding each term can help visualise why the indices are added.
- Add the Exponents: Focus on adding the indices when the base is the same. This is key to simplifying the expression correctly.
- Check Your Work: After simplifying, it's always good practice to check your work by expanding the expression to ensure it matches the original values.
Multiplying Indices – Extension
In multiplying indices, another important concept is the Power of a Power law. This rule comes into play when you have an index raised to another index, like $(n^a)^b$.
Power of a Power Law
The Power of a Power law states that when you raise a power to another power, you multiply the indices. This is written as $(n^a)^b = n^{a \cdot b}$.
For example, $(3^2)^4$can be expanded as $3^{2 \cdot 4} = 3^8$. This shows that you multiply the index outside the brackets with the index inside.
Understanding the Power of a Power law is crucial as it simplifies complex expressions and is a key component in algebra and higher-level maths.
Multiplying Indices – Summary
Let’s review what we learned about multiplication with indices in this text.
Key Points from This Text:
- To find the product of indices with the same base, keep the base and add the indices.
- This rule is based on expanding the exponential terms and counting the total number of times the base is multiplied.
- Mastery of this index multiplication is essential for advancing in algebra and other mathematical areas.
Feel free to complete interactive practice problems on this topic or complete our worksheets.
To explore exponents further, have a look at Exponents with Negative Bases and Division with Indices.
Multiplying Indices – Frequently Asked Questions
Multiplying Indices exercise
-
How else could we show this expression?
HintsThe base is the larger number, and the index is the smaller number on the top.
The base is the number being multiplied by itself, and the index tells us how many times the base is used as a factor in the multiplication.
Expanding an index means expressing it as repeated multiplication. For instance, for $a^n$, with $a$ as the base and $n$ as the index, you expand it by writing $a$ multiplied by itself $n$ times. Thus, $a^n$ expands to $a \times a \times \ldots \times a$, with $a$ appearing $n$ times.
Solution$(3 \times 3 \times 3 \times 3) \times (3 \times 3)$
-
Determine the rule for multiplying indices.
HintsWhen you multiply two numbers with the same base, you add their indices together and keep the base the same. For example, $a^m \times a^n = a^{m+n}$, where $a$ is the base and $m$ and $n$ are the indices.
Expanding the expressions can help you understand why we keep the base and add the indices when multiplying indices with the same base.
SolutionThe expression is written in exponential notation. Both terms have the same base of $\bf{3}$, but they have different indices. The rule for multiplying indices is to keep the base the same and add the indices.
The base will remain $3$, and the sum of indices will be found to find the solution index.
The final answer will be $\bf{3^6}$.
-
Simplify an expression.
HintsExpanding an index means writing it out as repeated multiplication. For example, if you have $a^n$, where $a$ is the base and $n$ is the index, you expand it by writing $a$ multiplied by itself $n$ times. So, $a^n$ becomes $a \times a \times \ldots \times a$, with $a$ appearing $n$ times.
There are 4 correct solutions.
Solution$(4^2) \times (4^4) = 4^{2+4}$
$(4^2) \times (4^4) = (4 \times 4) \times (4 \times 4 \times 4 \times 4)$
$(4^2) \times (4^4) = 4 \times 4 \times 4 \times 4 \times 4 \times 4$
$(4^2) \times (4^4) = 4^{6}$
-
Evaluate the expressions.
HintsWhen you multiply two numbers with the same base, you add their indices together and keep the base the same. For example, $a^m \times a^n = a^{m+n}$, where $a$ is the base and $m$ and $n$ are the indices.
Here is another example to help you.
$(1^3) \times (1^8)$
$1^{3+8}$
$1^{11}$
Solution$(6^3) \times (6^3) = 6^{3+3} = 6^6$
$(6^3) \times (6^6) = 6^{3+6} = 6^9$
$(3^3) \times (3^3) = 3^{3+3} = 3^6$
$(3^2) \times (3^1) = 3^{2+1} = 3^3$
-
What is the rule for multiplying indices?
HintsWhen you multiply two numbers with the same base, you add their indices together and keep the base the same. For example, $a^m \times a^n = a^{m+n}$, where $a$ is the base and $m$ and $n$ are the indices.
It may help you to expand each expression that is written in exponential notation. This will explain why we keep the base, and add the indices.
SolutionThe base is $\bf{8}$ and this number will stay the same.
The indices, $3$ and $2$ will be added $\bf{3+2}$.
$8^{3+2}$ which can simplify to $8^5$
-
Simplify an expression.
HintsWhen you multiply two numbers with the same base, you add their indices and keep the base unchanged, expressed as $a^m \times a^n = a^{m+n}$. This rule can be proven by expanding each index into repeated multiplication and observing that the total number of multiplications equals the sum of the indices.
You can only use the multiplication of indices rule, $a^m \times a^n = a^{m+n}$, when the bases are "like" or the same. If the bases are different, this rule does not apply.
Solution$5^3 \times 3^5 \times 5^4 \times 3^2$
Separate the terms by like bases.
$5^3 \times 5^4 = 5^7$
$3^5 \times 3^2 = 3^7$
$5^7 \times 3^7$ is the final solution because we can not combine these since the bases are unlike.
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?