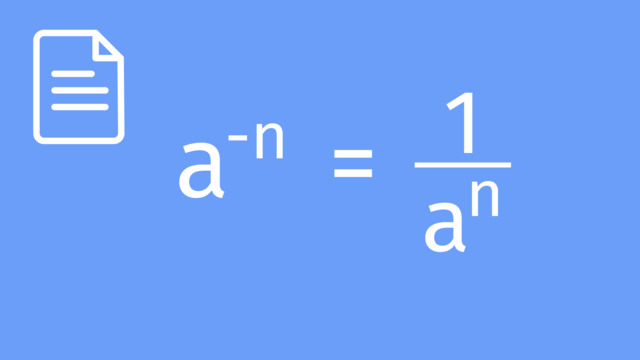Division with Indices
Learning text on the topic Division with Indices
Dividing Indices
In maths, indices, also called powers or exponents, are more than just numbers; they're keys to unlocking puzzles in the world around us. From calculating the decay of radioactive materials in science class to understanding how quickly a population of endangered species might decrease, Dividing Indices is an essential tool. This guide focuses on how to effectively divide numbers with the same base and their indices. We'll delve into this concept with relatable examples, demonstrating the rule: keep the base the same and subtract the indices.
If you are finding it hard to follow the text, we recommend consolidating your understanding of powers by watching this video: Understanding Powers of 10.
Understanding How to Divide Indices
The concept of dividing numbers written in standard form that have the same base follows a straightforward rule.
When dividing numbers written in standard form, or exponential notation, that have the same base, keep the base the same and subtract the indices.
For a clear example, let's look at this problem: $3^5 ÷ 3^2$.
Here, $3$ is the base, and $5$ and $2$ are the indices. By expanding these terms, we can see the logic behind subtracting the indices:
- $3^5 = 3 × 3 × 3 × 3 × 3$
- $3^2 = 3 × 3$
When dividing $3^5 ÷ 3^2$, we eliminate the two $3$s in $3^2$ from the five $3$s in $3^5$. This leaves us with three $3$s, or $3^3$. Thus, the expression simplifies to $3^{(5-2)} = 3^3$.
Dividing Indices – Steps to Simplify
| Divide | Expansion | Subtract the Indices | Simplify |
|---|---|---|---|
| $6^5 \div 6^3$ | $(6 × 6 × 6 × 6 × 6) \div (6 × 6 × 6)$ | $6^{(5-3)}$ | $6^2$ |
| $\dfrac{(n^5)}{(n^4)}$ | $\dfrac{(n × n × n × n × n)}{(n × n × n × n)}$ | $n^{(5-4)}$ | $n^1 = n$ |
Let's simplify some examples:
Dividing Indices – Application
Dividing Indices – Summary
Key Points from This Text:
- Dividing indices with the same base involves subtracting the index of the divisor from the exponent of the dividend.
- This rule simplifies the process of working with exponential expressions in division.
- Understanding this concept is crucial for both academic purposes and real-world applications, like analysing trends or growth rates.
Explore other topics, interactive problems, videos and printable worksheets on our website to further enhance your understanding of Division with Indices and other vital mathematical concepts.
To explore exponents further, have a look at Exponents with Negative Bases and Multiplication with Indices.
Dividing Indices – Frequently Asked Questions
Division with Indices exercise
-
Explain the rule for dividing indices.
HintsNotice in this example, the matching base is the variable $n$.
This stays the same.
Another way to understand dividing indices is to expand each index. Then it will make it clear that subtraction is used to find the final index.
SolutionWhen dividing indices that have the same base, the rule is keep the base the same and subtract the indices.
For example, $\dfrac{3^7}{3^3}$, the base is $\bf{3}$, so this stays the same. To find the quotient's index, subtract the indices: $\bf{7-3}$$=4$. The quotient is equal to $\bf{3^4}$.
-
How else could we show this expression?
HintsTo expand an index, the base is multiplied by itself the number of times the value of the index is.
For example, $4^3$ = $4 \cdot 4 \cdot 4$.
$\dfrac{5^6}{5^4}$
For the numerator, the base is $5$, and there are $6$ of them being multiplied. So, $5 \cdot 5 \cdot 5 \cdot 5 \cdot 5 \cdot 5$.
What is the base of the denominator, and how many times is that number being multiplied by itself?
$\cdot$ is used as a symbol for multiplication.
Solution$\dfrac{5^6}{5^4}$
The numerator has a base of $5$, and since the index is $6$, the $5$ is expanded as: $5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5$.
The denominator has a base of $5$, and the index is $4$, so the $5$ is expanded as: $5\cdot 5\cdot 5\cdot 5$
$\dfrac{5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5}{5\cdot 5\cdot 5\cdot 5}$
-
Divide the indices using the rule.
HintsIf you divide two numbers with the same base, you just subtract the smaller index from the bigger one and keep the base the same. For example, $a^m \div a^n = a^{m-n}$ when $a$ is a number and $m$ and $n$ are the indices.
Here is an example to help you.
$\dfrac{2^7}{2^6}$
$2^{7-6}$
$2^1=2$
Solution$\dfrac{5^9}{5^3}$
$5^{9-3}$
$5^6$
-
Apply the rule to evaluate expressions.
HintsWhen you divide two numbers with the same base, you keep the base the same and subtract the indices.
If it helps you to better understand the rule, first expand the expression and then cross off pairs.
Solution- $\frac{4^7}{4^3} = 4^{7-3} = 4^4$
- $\frac{4^4}{4} = 4^{4-1} = 4^3$
- $\frac{3^6}{3^2} = 3^{6-2} = 3^4$
- $\frac{4^8}{4^2} = 4^{8-2} = 4^6$
-
Apply the rule for dividing indices.
HintsWhen you divide two numbers with the same base, you keep the base the same and subtract the indices.
The base in this example is $3$, and then the indices are subtracted, $6-5$.
SolutionThe base is $2$.
The indices will be subtracted $8-2$.
The final solution will be $2^6$.
-
Find the solution by applying the rule.
HintsWhen you type in your answer, use the $x^a$ button on the toolbar to create an index.
If you divide two numbers with the same base, you just subtract the smaller index from the bigger one and keep the base the same.
For example, $a^m \div a^n = a^{m-n}$ when $a$ is a number and $m$ and $n$ are the indices.
Solution$\begin{array}{l}\frac{5^5}{5^2}=5^{5-2}=5^3\\ \\ \frac{8^2}{8}=8^{2-1}=8\\ \\ \frac{9^7}{9^2}=9^{7-2}=9^5\\ \\ \frac{x^6}{x^4}=x^{6-4}=x^2\end{array}$
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?