Equivalent Fractions
Do you want to learn faster and more easily?
Basics on the topic Equivalent Fractions
Equivalent Fractions – Definition
In this learning text we will be looking at equivalent fractions and how to find equivalent fractions. You may already know from our previous videos what a fraction is. Let’s look at the recap of the definition of what fractions and equivalent fractions are.
Fractions always represent a part of a whole. For example, if a pizza is divided into four equal pieces, one piece is called $\frac{1}{4}$ of a whole pizza.
Equivalent fractions are fractions which have the same value but are represented with a different numerator and denominator.
Equivalent fractions are created by breaking a whole into smaller equal parts. For example, the equivalent fractions visual diagram below is showing a whole as a fraction of $\frac{2}{2}$ and another fraction which is still one whole as a fraction $\frac{8}{8}$. So, the fractions $\frac{2}{2}$ and $\frac{8}{8}$ are equivalent fractions.
To create equivalent fractions, we can increase the number of pieces by multiplying the numerator and the denominator by the same n factor.
In mathematics, we use a multiplication expression to represent an equivalent fraction. The left-hand side of the expression represents our fraction and the right-hand side of the expression represents an equivalent fraction multiplied by n, where n represents any number. The equal sign shows that both sides of the expression are equal to each other. The bigger the number we multiply the fraction by, the more equal parts the whole has.
| original fraction | how to find the equivalent fraction |
|---|---|
| $\frac{a}{b}$ | $\frac{a x n}{b x n}$ |
Now, we can look at some examples for better understanding of equivalent fractions and after that you can practise equivalent fractions on the worksheet or play equivalent fractions bingo.
Equivalent Fractions – Example 1
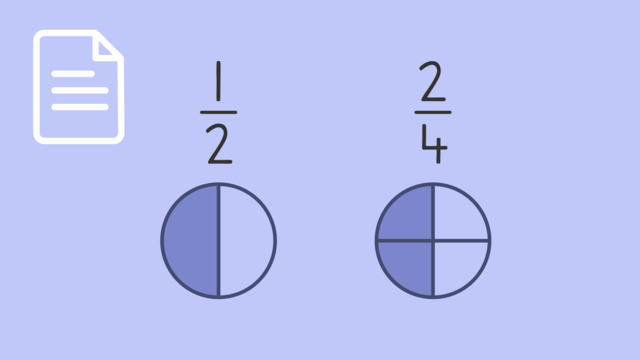
Let’s look at our first fraction, which is $\frac{1}{2}$. If we multiply the numerator and the denominator by two, we have generated an equivalent fraction which is $\frac{2}{4}$. The size of these parts is different, but the size of the whole remains the same.
| fraction | equivalent fraction |
|---|---|
| $\frac{1}{2}$ | $\frac{2}{4}$ |
Equivalent Fractions – Example 2
In our second example, we are looking at $\frac{3}{4}$. Let’s multiply the numerator and the denominator of the fraction by three, so we will get $\frac{9}{12}$. In this example, the n equals three.
We can also use a different factor; this time let’s multiply the numerator and the denominator of $\frac{3}{4}$by six, so we will get an equivalent fraction which is $\frac{18}{24}$. This time, the n factor equals six.
We can change the n factor for any other number, we just must remember to multiply the numerator and the denominator by the same n factor.
| fraction | equivalent fraction |
|---|---|
| $\frac{1}{2}$ | $\frac{2}{4}$ |
Equivalent Fractions – Summary
How do we generate or create an equivalent fraction? Look at the summary below:
- Equivalent fractions are fractions that have the same value but have different numbers in the numerators and denominators.
- Equivalent fractions are created by breaking a whole into smaller equal parts and having a greater number of pieces.
- We can increase the number of parts in a fraction by multiplying the numerator and the denominator by the same factor.
- Use the multiplication expression.
- Pick a number and then multiply the numerator and denominator by the chosen factor.
Frequently Asked Questions about Equivalent Fractions
Transcript Equivalent Fractions
“B.... two-thirds!!” It’s fraction night down at the bingo hall and Axel and Tank are excited to try to win the night’s top prize which is a trip for two to Submersive Studios! In order to be the first to fill their bingo card, they need to find: Equivalent Fractions. Equivalent fractions are fractions that have the same value but have different numbers in the numerators and denominators. They can be created by breaking the whole into smaller parts and having a greater number of pieces. We increase the number of parts in the fraction by multiplying the numerator and denominator by the same factor. One-half and two-quarters are an example of equivalent fractions. In one half, the whole is divided into two larger parts and one of the halves is shaded in. By multiplying both the numerator and the denominator in one half, by two, we make two quarters. The denominator has been multiplied by two to make four, so the whole is now grouped into four parts and the numerator has been multiplied by two, equalling two, so there are now two parts shaded in. We could continue generating fractions equal to one -half by multiplying the numerator and denominator by other factors. Even though the size of the parts differ, the amount shaded and the size of the whole remain the same and therefore so does the value of the fraction. The next fraction called out is three-quarters. To find an equivalent fraction on his card, Axel is going to multiply the numerator and denominator by three. In the denominator, we multiply four by three, which makes twelve. In the numerator we multiply three by three, which equals nine. Nine-twelfths is equivalent to three-quarters. Tank decides to multiply the numerator and denominator in three-quarters by six. Four times six equals twenty-four and three times six is eighteen. Three-quarters is also equivalent to eighteen twenty-fourths. Five-sixths is the next fraction called. Axel is going to make an equivalent fraction by multiplying the numerator and denominator by five. What is the equivalent fraction? Twenty-five thirtieths. Tank decides to multiply the numerator and denominator by eight. What equivalent fraction did he make? Forty, forty-eighths. These aren’t the only fractions that would be equivalent. In the comments section, share other fractions that are also equivalent to five-sixths and what you multiplied the numerator and denominator by to make them. “G…four-fifths!” While Axel and Tank look for an equivalent fraction on their card, let’s review. Remember, equivalent fractions are fractions that have the same value but have different numbers in the numerators and denominators. They can be created by breaking the whole into smaller parts and having a greater number of pieces. We increase the number of parts in the fraction by multiplying the numerator and denominator by the same factor. "Bingo!" "Grandma?!"
Equivalent Fractions exercise
-
What is an equivalent fraction?
HintsAll fractions are part of a whole.
Think about the pieces of a fraction. Are all pieces the same size?
If the numerator and denominator of $\frac{1}{2}$ are multiplied by 2, what equivalent fraction do we get?
SolutionEquivalent fractions are fractions that have the same value but have different numbers in the numerators and denominators. An example of a fraction equivalent to $\frac{1}{2}$ is $\bf{\frac{2}{4}}$.
-
How have these equivalent fractions been created?
HintsEquivalent fractions represent the same number, but have different size pieces.
Use the image to help you.
The fraction to the left is $\dfrac{1}{2}$, what do you notice about the relationship between that and the fraction represented on the right, $\dfrac{4}{8}$?
We must multiply the numerator and the denominator of the first fraction by the same number to create a new equivalent fraction.
SolutionBy multiplying the fraction's numerator and denominator by the same factor, we create equivalent fractions.
The fraction represented on the left is $\dfrac{1}{2}$ and the fraction represented on the right is $\dfrac{4}{8}$. To create this equivalent fraction, we multiply both the numerator and denominator of $\frac{1}{2}$ by 4.
1 x 4 = 4
2 x 4 = 8
Therefore $\frac{4}{8}$ is an equivalent fraction.
-
Which is the equivalent fraction?
HintsRemember, you have to multiply both the numerator and the denominator by the same number.
Think about how you create equivalent fractions.
Draw models to help you.
If we multiply the numerator and denominator of $\frac{6}{9}$ by 2 we get $\frac{12}{18}$. What would we get if we multiply them by 3?
SolutionThe correct answer is $\frac{18}{27}$. You multiply both numerator and denominator by 3.
6 x 3 = 18
9 x 3 = 27
-
Identify equivalent fractions.
HintsRemember, in order to make equivalent fractions, you must multiply the numerator and the denominator by the same number.
For example, the fraction $\frac{3}{9}$ could have both the numerator and denominator multiplied by $10$ to find an equivalent fraction.
$\frac{3\ \ \ \ \times 10}{9\ \ \ \ \times 10}=\ \frac{30}{90}$
Multiply both the numerator and denominator of $\frac{3}{9}$ by other factors to find other equivalent fractions.
SolutionThe following fractions are equivalent to $\frac{3}{9}$
- $\frac{12}{36}$- multiply the numerator and denominator by 4
- $\frac{15}{45}$- multiply the numerator and denominator by 5
- $\frac{9}{27}$- multiply the numerator and denominator by 3
- $\frac{18}{54}$- multiply the numerator and denominator by 6
-
Can you find the equivalent fractions?
HintsThink about what you would multiply the numerator and denominator by. Remember, it has to be the same number.
Look for the same value, just different size piece.
In the image here you notice that $\frac{1}{2}$ and $\frac{4}{8}$ are the same size, but are split up into different sized groups. These fractions are equivalent.
SolutionEquivalent Fraction Solutions:
- $\frac{3}{6}$ = $\frac{9}{18}$
- $\frac{1}{8}$ = $\frac{2}{16}$
- $\frac{2}{8}$ = $\frac{6}{24}$
- $\frac{1}{4}$ = $\frac{4}{16}$
-
How can we determine which fractions are equivalent?
HintsRemember equivalent means equal. They will not have the same number or size pieces, but they will take up the same amount of space.
When finding equivalent fractions, you multiply the numerator and denominator by the same number. For example, if we had the fraction $\frac{3}{5}$ and multiplied both parts by 3, we get $\frac{9}{15}$. These are equivalent.
There can be multiple equivalent fractions for one given model. You just have to think about what are you multiplying by.
SolutionIn order to find the correct pairs, you have to think about what you would multiply the numerator and denominator by in order to make the fractions equivalent.
Let's look at the first pair as an example: The model shows $\frac{4}{8}$. If you multiply both the numerator and denominator by 4, you get the fraction $\frac{16}{32}$ and these fractions are equivalent.
Here are the remaining pairs and their matches: The model $\frac{2}{3}$ is equivalent to $\frac{4}{6}$ because you multiply by 2.
The model $\frac{3}{4}$ is equivalent to $\frac{15}{20}$ because you multiply by 5.
The model $\frac{5}{7}$ is equivalent to $\frac{10}{14}$ because you multiply by 2.
