Equivalent Fractions
Do you want to learn faster and more easily?
Basics on the topic Equivalent Fractions
Equivalent Fractions
What are equivalent fractions? You may have already learnt about fractions, what they are and what they look like, but in this equivalent fractions video you will learn all about how to find and work out equivalent fractions. Below you will find an in depth explanation of equivalent fractions with examples to help. Becoming confident with equivalent fractions in year 4 and developing further on what you may have learnt in year 3 about equivalent fractions will help you become successful in mastering fractions!
Equivalent Fractions – Definition
What does it mean when two fractions are equivalent? A simple definition for equivalent fractions is as follows:
The word equivalent means the same, so an equivalent fraction is the same fraction but written differently. Equivalent fractions are fractions that are from the same whole with numerators and denominators different from one another but identical in value.
Identifying Equivalent Fractions
How do you find equivalent fractions? Models help us to find equivalent fractions. We can compare the value of different fractions from the same whole using models called fraction bars. Fraction bars show us whether or not the fractions are equivalent, or equal in value. When thinking about how to explain equivalent fractions, using the method: draw and label two models that show equivalent fractions, can be helpful.
Assuming the fractions are from the same whole, when two fractions are equivalent it means that their numerator and denominator are different from each other but the value of the fraction is the same.
Equivalent Fractions – Example
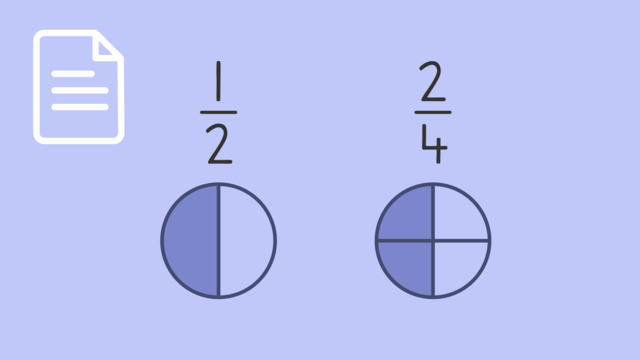
Let’s begin by thinking about equivalent fractions for $\frac{1}{2}$ such as one-half and two-quarters. To determine if they are equal in value, the first step is to draw equivalent fractions models for both fractions. Represent the first fraction by shading that bar to represent one-half.
Then, represent the second fraction on a bar of identical size by shading it to represent two-quarters.
Finally, compare the shaded values of both bars to see if fractions are equivalent. Each fraction bar has the same quantity shaded, which means they are equal in value. Since they are equal in value, the fractions one-half and two quarters are equivalent. A similar method can also be used to find equivalent fractions for $\frac{3}{4}$.
Let’s try one more example using four-sixths and two-fifths to tell whether the fractions are equivalent. We will see if they are equivalent fractions with models. To determine if they are equal in value, we will draw the fraction bar to represent the first fraction. Shade that fraction bar to represent four-sixths.
Then, draw a second fraction bar of identical size to represent the second fraction. Shade that fraction bar to represent two-fifths.
Finally, compare the shaded value of both bars. Since the shaded values are different, four sixths and two fifths are not equivalent fractions.
Equivalent Fractions – Summary of Steps
What does it mean when two fractions are equivalent? Assuming the fractions are from the same whole, when two fractions are equivalent it means that their numerator and denominator are different from each other but the value of the fraction is the same. As an introduction to equivalent fractions, we model equivalent fractions. We can compare the value of different fractions from the same whole using models called fraction bars. Fraction bars show us whether or not the fractions are equivalent, or equal in value. To determine if two fractions from the same whole are equivalent:
First, draw and shade a fraction bar to represent the first fraction.
Then, draw and shade another fraction bar of identical size to represent the second fraction.
Finally, compare the shaded values of both bars.
If they are equal in value, the fractions are equivalent.
| Step # | What to do |
|---|---|
| 1 | Draw and shade a fraction bar to represent the first fraction. |
| 2 | Draw and shade another fraction bar of identical size to represent the second fraction. |
| 3 | Compare the shaded values of both bars. |
| 4 | If they are equal in value, the fractions are equivalent. |
Below is an overview of some common equivalent fractions which you might encounter frequently.
| Original fraction | Possible equivalent fractions |
|---|---|
| Equivalent fractions for $\frac{1}{3}$ | $\frac{2}{6}$ $\frac{3}{9}$ $\frac{4}{12}$ |
| Equivalent fractions for $\frac{1}{4}$ | $\frac{2}{8}$ $\frac{3}{12}$ $\frac{4}{16}$ |
| Equivalent fractions for $\frac{1}{2}$ | $\frac{2}{4}$ $\frac{3}{6}$ $\frac{4}{8}$ $\frac{5}{10}$ |
Equivalent Fractions – Practice
Now that you have looked at the examples of equivalent fractions, you can do some more practise using the interactive exercises and worksheets on equivalent fractions to develop your understanding of equivalent fractions for ks2. It can be helpful to also have a look at the equivalent fractions worksheet in year 5 or year 6, to consolidate understanding. Before you know it you will be an expert at finding equivalent fractions!
Transcript Equivalent Fractions
Axel and Tank are babysitting Axel’s little brother, Odell. Axel's mum left very strict instructions for them to follow. Odell needs half a bottle in the morning, four-sixths of a bottle in the afternoon and one-quarter of a bottle before bed. There's only one problem- his mum took the nappy bag with all the bottles! In order to feed Baby Odell, Axel and Tank need to find equivalent fractions. Equivalent fractions are fractions from the same whole with numerators and denominators different from one another but identical in value. We can compare the value of different fractions from the same whole using fraction bars. Fraction bars show us whether or not the fractions are equivalent, or equal in value. Let's use Baby Odell's first bottle to explain. Mum's instructions say that he needs half a bottle straight away, but Axel and Tank are using a jug the same size filled two-quarters of the way to the top. To determine if one-half and two-quarters are equivalent First, draw a fraction bar to represent the first fraction. Shade the bar to represent one-half. Then, draw a fraction bar of the identical size to represent the second fraction. Shade the bar to represent two quarters. Finally, compare the shaded values of both bars. Each fraction bar has the same quantity shaded, which means they are equal in value. Since they are equal in value, the fractions one-half and two quarters are equivalent. Axel and Tank can feed baby Odell the jug that is filled two-quarters of the way to the top, because it is the same amount as Mum instructed. For the next feed, Mum said Odell needs four-sixths of a bottle, but they are using a same-sized jug filled to two-fifths. To determine if four-sixths and two-fifths are equivalent: draw the fraction bar to represent the first fraction. Shade the fraction bar to represent four-sixths. Then, draw a fraction bar of identical size to represent the second fraction. Shade the fraction bar to represent two-fifths. Finally, compare the shaded value of both bars. Since the shaded values are different, four-sixths and two-fifths are not equivalent. Axel and Tank try using another same-sized jug filled to two-thirds this time. What should they do first? They should draw and shade the fraction bar to represent two-thirds. Finally, they should compare the shaded value of four-sixths and two-thirds. Since they are the same, four-sixths and two-thirds are equivalent. Axel and Tank can feed Baby Odell this jug because it is the same amount that Mum instructed. For the last bottle, Mum said to give him one-quarter of a bottle, but Axel and Tank are using a same-sized jug filled to four-sixteenths. Pause the video here to determine if one-quarter and four-sixteenths are equivalent. Now let's check our work! We draw and shade the fraction bar to represent one-quarter. Then, we draw and shade another fraction bar to represent four-sixteenths. The last step is to compare the shaded quantities of both bars. These fractions are equivalent because they show the same value. Axel and Tank can feed Odell the last jug because it's the same amount as Mum instructed. "Peeee yew! What is that smell?" Before we can work out where the smell is coming from, let's remember. Equivalent fractions are fractions from the same whole, with numerators and denominators different from one another, but identical in value. We can compare the value of different fractions from the same whole using fraction bars. Fraction bars show us whether or not the fractions are equivalent, or equal in value. To determine if two fractions from the same whole are equivalent, first, draw and shade a fraction bar to represent the first fraction. Then, draw and shade another fraction bar of identical size, to represent the second fraction. Finally, compare the shaded values of both bars. If they are equal in value, the fractions are equivalent. "Oh no, Axel. I think I worked out where the smell is coming from." "It's ok...my mum got home just in time!"
Equivalent Fractions exercise
-
Can you match the fraction to the picture?
HintsLook at the numerator (top part of the fraction). It should match the amount filled in.
Look at the denominator (bottom part of the fraction). It should match the number of equal parts.
This bottle shows $\frac{3}{4}$.
The bottle is split into 4 equal parts. The milk is filled to the 3rd line.
SolutionThis image shows the correct fraction for each bottle.
The denominator is the number of equal parts your whole is broken into.
The denominator in $\frac{2}{3}$ is 3
The bottle is broken into 3 equal parts.The numerator is the number of parts shaded, filled in and taken from the whole.
The numerator in $\frac{2}{3}$ is 2 The bottle shows the milk filled to 2 of the 3 parts. -
Find the equivalent fraction.
HintsLook at the fraction bar. What is equivalent to $\frac{4}{6}$ ?
Equivalent fractions show the same value.
SolutionEquivalent fractions represent the same value with different numerators and denominators .
In order to determine if fractions are equivalent, you can draw fraction bars.
Each bar should represent each fraction.
If the shaded portion of each fraction bar is equal to each other, then they are equivalent .Even though the bottles are broken into different equal parts, because the bottles are the same size, when the milk is filled to the same height, they have the same amount.
-
Sort the fractions into the correct label.
HintsEquivalent fractions represent the same value.
Both rectangles have $\frac{1}{2}$ shaded and the amount shaded is the same.
SolutionEquivalent fractions represent the same value.
Equivalent fractions have different numerators and denominators. -
Match the fraction bar to the equivalent fraction.
HintsDraw a fraction bar for the given fraction.
The shaded portion of the fraction bars should be the same if they are equivalent.
How many fifths are equivalent to $\frac{4}{10}$ ?
SolutionEquivalent fractions have different numerators and denominators but represent the same value.
To determine if fractions are equivalent, you can create fraction bars.
If the shaded portion for each fraction bar is the same size, that means the fractions are equivalent.
-
Make the fractions equivalent.
HintsLook at the fraction bars, what fraction is equivalent to two thirds?
How many sixths do you need to colour to match $\frac{2}{3}$ ?
SolutionTo determine if fractions are equivalent, you can draw fraction bars.
First, show $\frac{2}{3}$ in a fraction bar.
Second, make a fraction bar divided into six equal parts.
Third, colour each sixth until it is equivalent in size to $\frac{2}{3}$ .
-
Select which fraction is equivalent.
HintsDraw fraction bars to determine if the fractions are equivalent.
To make fractions equivalent, the shaded part of the fraction bars should be equal.
$\frac{3}{6}$ is the same as a half. What other fraction is equivalent to a half?
SolutionEquivalent fractions are fractions with different numerators and denominators but represent the same value.
You can draw fraction bars to determine if fractions are equivalent.
