Equations with Addition and Subtraction
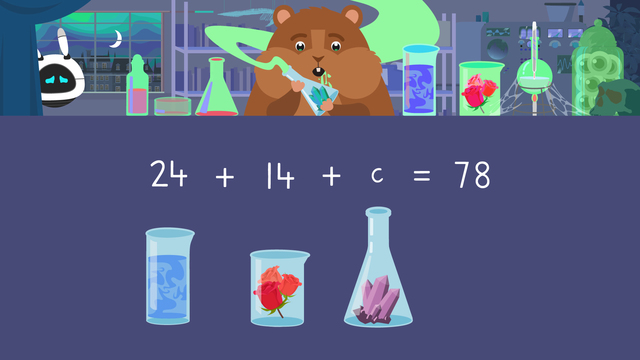

Basics on the topic Equations with Addition and Subtraction
Solving Equations by Adding or Subtracting
What is an Equation? An equation tells us that the expression on either side of the equals sign is equal to the other. Sometimes, when writing an equation, you may have an unknown value that you need to find. A variable is a letter used to represent the value that we're looking for.
Equations can be used to solve addition and subtraction word problems by following these steps:
| Step # | What to do |
|---|---|
| 1 | Read the word problem |
| 2 | Highlight the important information |
| 3 | Identify the operation |
| 4 | Write the equation using a variable to represent the unknown value |
| 5 | Solve the equation |
Solving Equations by Adding or Subtracting – Example
How do you solve one step equation word problems addition and subtraction or 2 step addition and subtraction word problems? Or ones with even more steps? Let’s take a look at the example from the video:
In order to reverse the experiment, Imani needs seventy-eight ingredients altogether. The directions say they need twenty-four jars of mist and fourteen rose petals. The rest of the ingredients they need are crystals. How many crystals does Imani need? Remember, when solving these yourself, highlight keywords for addition and subtraction word problems.
Our equation is: twenty-four jars of mist plus fourteen rose petals plus c equals seventy-eight because if we add all of the ingredients together, the total number they need is seventy-eight.
Let’s Solve
First, we add twenty four jars of mist and fourteen rose petals to get thirty-eight, but we still don't know how many crystals we need!
This is an addition equation, but since we do not know the value of c, we need to practise solving an addition equation using inverse operations.
The inverse operation of addition is subtraction, so we subtract thirty-eight from the number of ingredients in total, which is seventy-eight. Seventy-eight minus thirty-eight is forty, and we write the answer using the variable c equals forty.
Solving Equations by Adding or Subtracting – Summary
Remember an equation tells us that the expression on either side of the equals sign is EQUAL to the other. Equations can be used to solve word problems. When writing the equation we use a variable to represent the unknown value. Sometimes when solving equations with addition and subtraction you may have to use the inverse operation to find the answer. Always include the variable in your answer using an equals sign.
Want some more practice for addition and subtraction word problems? After the video, you can find addition and subtraction equation worksheets along with other activities, and interactive exercises for KS2.
Transcript Equations with Addition and Subtraction
Mr. Squeaks has travelled through time and is conducting experiments in his lab. "Mr. Squeaks! What have you done?!" "Now I am Doctor Squeaks, if you want Mr. Squeaks back, you'll have to follow these directions!" In order for Imani to change Doctor Squeaks back to Mr. Squeaks, they need to follow the directions and solve Equations with Addition and Subtraction. An equation tells us that the expression on either side of the equals sign is EQUAL to the other. Equations can be used to solve word problems.
First, read the word problem.
As you read, think; 'what do I need to find?' and highlight the question you need to solve!
For example, in order to reverse the experiment, Imani needs seventy-eight ingredients altogether. The directions say they need twenty-four jars of mist and fourteen rose petals. The rest of the ingredients they need are crystals. How many crystals does Imani need?
Here we highlight “How many crystals does Imani need?”, because it asks us to find how many crystals are needed to reverse the experiment.
Now, reread and think; 'What is the important information?'
While re-reading, highlight keywords, numbers, or units of measurement, that will help to answer the question.
In the first sentence, highlight seventy-eight ingredients altogether, because this tells us the total number of ingredients they need.
In the next sentence, highlight twenty-four jars of mist and fourteen rose petals, because this tells us how many of each ingredient they need.
Also highlight, "the rest of the ingredients they need are crystals", because that is the unknown value, or what we're trying to work out.
Then, identify the operation.
We can't identify the operation just yet, so we move on to the next step.
The next step is to write the equation. To do this we will use a letter to represent the unknown amount.
We call this a VARIABLE which is a letter used to represent the value that we're solving for.
Our equation is: twenty-four jars of mist plus fourteen rose petals plus
"Mr. Squeaks! You're back, no more Dr. Squeaks!" "What are you talking about Imani? Let's get you back home."
Equations with Addition and Subtraction exercise
-
Complete the sentences.
HintsHere's an example of an equation.
The 'c' in this equation is a variable.
SolutionEquations tell us that the expression on either side of the equals sign is equal to the other.
Equations can be used to solve word problems.
We use variables to represent the unknown values in equations.
-
Solve the story problem.
HintsReread the problem and think: what is the important information?
Write the equation using a variable to represent the unknown value. Here, we could use 'r' to represent the rose petals.
Add any numbers together first.
To solve for the variable, do the opposite operation to the answer. For example in 4 + b = 5, you would subtract 5 - 4 to solve for b.
SolutionAfter highlighting the important information shown, this is the equation with the variable solved:
64 = 31 + 12 + r
31 + 12 = 43
64 = 43 + r
64 - 43 = r
64 - 43 = 21
Therefore r = 21
So, 21 rose petals were needed. -
What does x equal in each equation?
HintsRemember, you are solving for the variable, or the letter. In all of these equations it is x.
Add any numbers together first.
To solve for the variable, do the opposite operation to the answer.
For example in 4 + x = 5, you would subtract 5 - 4 to solve for x.
Another strategy to check your answer, is to plug in the number for x to see if it's correct.
Solutionx + 10 = 25
x = 25 - 10
x = 1537 = 26 + x
37 - 26 = x
x = 1113 + 22 + x = 42
13 + 22 = 35
35 + x = 42
x = 42 - 35
x = 757 = 32 + 12 + x
32 + 12 = 44
57 = 44 + x
57 - 44 = x
x = 13 -
Solve each word problem.
HintsReread the problem and think: what is the important information?
Write the equation using a variable to represent the unknown value.
Add any numbers together first.
To solve for the variable, do the opposite operation to the answer. For example in 4 + b = 5, you would subtract 5 - 4 to solve for b.
SolutionFor the first problem:
27 + 36 + x = 72
27 + 36 = 63
63 + x = 72
x = 72 - 63
72 - 63 = 9
Therefore x = 9, so 9 jars of mist were needed.
For the second problem:
72 = 22 + 32 + x
22 + 32 = 54
72 = 54 + x
72 - 54 = x
72 - 54 = 18
Therefore, x = 18 so 18 leaves were needed. -
How many bananas does Mr. Squeaks have?
HintsRemember, you are solving for the variable, or the letter.
Add any numbers together first.
To find what b equals, we first need to add 13 + 25 which equals 38. What do we do now?
Now we can subtract 38 from 50 to find the answer.
Solution13 + 25 + b = 50
13 + 25 = 38
38 + b = 50
b = 50 - 38
50 - 38 = 12
Therefore b = 12.Mr. Squeaks has 12 bananas.
-
Have Mr. Squeaks and Imani calculated their equations correctly?
HintsReread the problem and think: what is the important information?
Write the equation using a variable to represent the unknown value.
Add any numbers together first.
To solve for the variable, do the opposite operation to the answer. For example in 4 + b = 5, you would subtract 5 - 4 to solve for b.
SolutionFor the first smoothie:
17 + 44 + b = 75
17 + 44 = 61
61 + b = 75
b = 75 - 61
75 - 61 = 14
Therefore, b = 14, so that answer was correct.
For the second smoothie:
64 = 32 + 18 + r
32 + 18 = 50
64 = 50 + r
64 - 50 = r
64 - 50 = 14
Therefore, r = 14, not 15, so that answer was incorrect.
For the last smoothie:
52 = 19 + 27 + i
19 + 27 = 46
52 = 46 + i
52 - 46 = i
52- 46 = 6
Therefore, i = 6, not 16, so that answer was incorrect.
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?
















