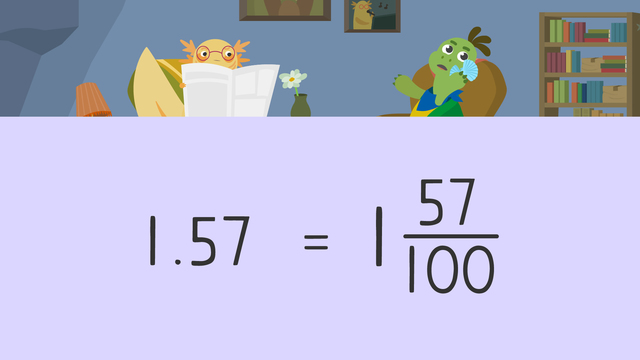Decimals Greater than 1 as Fractions — Let's Practice!

Decimals Greater than 1 as Fractions — Let's Practice! exercise

• Match the decimal to a fraction.

  Hints

  Write each place value as a fraction.

  After you write each place value as a fraction, multiply the numerator and denominator so every denominator equals 100. Add the numerators together.

  $\frac{100}{100}$ + $\frac{30}{100}$ + $\frac{8}{100}$ = $\frac{138}{100}$ = 1 $\frac{38}{100}$

  Solution

  Write each place value as a fraction.

  • For example: 1.67 = $\frac{1}{1}$ + $\frac{6}{10}$ + $\frac{7}{100}$

  After you write each place value as a fraction, multiply the numerator and denominator so every denominator equals 100.

  • For example: 1.67 = $\frac{100}{100}$ + $\frac{60}{100}$ + $\frac{7}{100}$

  When you add all of the numerators, you find the equal fraction.

  • For example: 1.67 = $\frac{167}{100}$

  We can then convert this to a mixed number: 1 $\frac{67}{100}$.

  _____________________________

  • 2.32 = 2$\frac{32}{100}$
  • 3.80 = 3$\frac{8}{10}$
  • 1.05 = 1$\frac{5}{100}$

• True or False?

  Hints

  Write each place value as a fraction.

  Multiply the fractions so they all have a common denominator. Add the numerators together.

  Convert to a mixed number.

  Double check place value. Are the correct digits in the tenths or hundredths places?

  Solution

  • 2.67 = 2$\frac{67}{100}$ true
  • 4.07 = 4$\frac{7}{100}$ true
  • 3.2 = 3$\frac{2}{100}$ false. 3.2 = 3$\frac{2}{10}$
  • 5.92 = 5$\frac{92}{10}$ false. 5.92 = 5$\frac{92}{100}$

• Can you write decimals and fractions?

  Hints

  Number 1 is missing the ones place. Which number is in the ones place?

  5.47 = $\frac{500}{100}$ + $\frac{40}{100}$ + $\frac{7}{100}$

  Number 2 is missing the decimal. How can you convert 3$\frac{21}{100}$ to a decimal?

  3$\frac{21}{100}$ = $\frac{300}{100}$ + $\frac{20}{100}$ + $\frac{1}{100}$

  What is this as a decimal?

  Solution

  1. 5.47 = 5$\frac{47}{100}$
  2. 3.21 = 3$\frac{21}{100}$

• Convert the fraction into a decimal.

  Hints

  Work out which place value each digit is in.

  In 2$\frac{6}{10}$, the 2 is in the ones place and the 6 is in the tens place.

  As an example, 1$\frac{6}{10}$ converts to 1.6.

  Solution

  2$\frac{6}{10}$ = 2.6
  5$\frac{8}{10}$ = 5.8
  4$\frac{4}{100}$ = 4.04
  9$\frac{73}{10}$ = 9.73

• Match the fraction to the correct decimal.

  Hints

  Write each place value as a fraction. Make sure to check the tenths and hundredths place.

  The 2 is in the tenths place. The 7 is in the hundredths place.

  Put the parts of the mixed number into a place value chart.

  Solution

  1 $\frac{27}{100}$ = 1.27

  • There is a 1 in the ones place. $\frac{100}{100}$
  • There is a 2 in the tenths place. $\frac{20}{100}$
  • There is a 7 in the hundredths place. $\frac{7}{100}$

• True or False?

  Hints

  There are four place values in 2.369. What are they?

  Use the chart to help you. Create fractions for each place value. The next place value after hundredths is thousandths, so the fraction that represents the 9 in the thousandths place is $\frac{9}{1000}$

  Solution

  True.

  2$\frac{369}{1000}$ = 2.369