Decimals Greater than 1
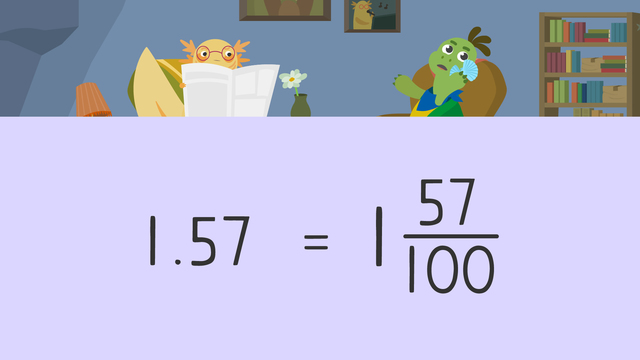

Basics on the topic Decimals Greater than 1
Decimals Greater than 1 as Fractions
When we have a number that is greater than 1 and written as a decimal, we can convert it so that it is written as a fraction. To write decimals greater than one as fractions, it is important to identify the place value for decimals greater than 1. This helps to know what the denominator is.
Decimals Greater than 1 as Fractions – Example
To write decimals greater than one as fractions, it is important to identify the place value for decimals greater than 1. This helps to know what the denominator is. Let’s look at the number one and fifty-seven hundredths.
The first step is to set up a place value chart to the hundredths place, and write the number on the place value chart. This means one goes in the ones place, five goes in the tenths place, and seven goes in the hundredths place.
Next, we write all the numbers as a fraction. One whole can stay as it is. Five tenths as a fraction is five over ten, and seven hundredths as a fraction is seven over one hundred.
Then, we need to convert the fractions to have common, or the same, denominators. In this example, we will convert all fractions to have the denominator one hundred. We multiply the numerator and denominator by ten for five over ten to get fifty over one hundred. Seven over one hundred does not need converting.
Now, we add all the fractions together. The denominator remains one hundred, and we add fifty plus seven to give us fifty-seven for the numerator.
We then add the one whole to make one and fifty seven hundredths.
This means that one point five seven as a fraction is one and fifty-seven hundredths.
Decimals Greater Than 1 – Summary
Decimals greater than 1 are numbers greater than one with a decimal place. You can display decimals greater than 1 as fractions or as mixed numbers. When you need to represent numbers with decimals, you can use a place value chart to the hundredths place or multiply the number by 100. Follow these steps to identify the place value of decimals:
| Step # | What to do |
|---|---|
| 1 | Set up a place value chart to the hundredths place and write down the number. |
| 2 | Write all the numbers as a fraction. One whole is one over one as a fraction. |
| 3 | Convert the fractions to have common denominators. Then add the numerators. |
| 4 | Since the numerator will be greater than one hundred, you can rewrite the fraction as a mixed number. |
After watching the video you will find more interactive exercises, worksheets and further activities concerning decimals greater than 1 to practise converting decimals greater than one to fractions.
Transcript Decimals Greater than 1
"Thanks for the help, Michelle." "Basically, we need to convert the decimals on your lock screen to fractions to unlock it!" "Fine, I just want to use my new shell phone." Let's help Axel unlock Tank’s new shell phone by learning all about decimals greater than one as fractions. Decimals represent a whole number and a fractional part of a whole number. Decimals greater than one can be converted, or changed, into fractions with ten or one hundred as the denominator. Let's look at the first number that we need to convert to unlock Tank's new shell phone. We have one point five seven. When converting decimals to fractions, first, write the number on a place value chart. The digit in the ones column is one, this represents one whole, so we can leave this as one here. The five is in the tenths column, so we can write five tenths like this. In the hundredths place we have seven, so we can write seven hundredths as a fraction like this. Next, we will convert these fractions so that they both have the same denominator, then we can add them together. Convert all fractions to hundredths, the greatest denominator here. To convert tenths into hundredths we need to multiply by ten. Remember that when we convert a fraction, we always multiply the numerator and the denominator by the same thing. Five times ten is fifty and ten times ten is one hundred. Seven hundredths already has one hundred for a denominator so it stays the same. Next, find the sum. We need to add the numerators, fifty plus seven. Fifty plus seven is fifty-seven. So we have one and fifty-seven hundredths. One point five seven is the same as one and fifty-seven hundredths. Now the first code has been entered, let's look at the other code. The decimal is three point four. What is the first step? Write the decimal on to the place value chart and then write the fractions below. Three is in the ones column, so we can write three here and four is in the tenths column, so we can write four-tenths as a fraction like this. Next, put the numbers together, three plus four-tenths is three and four tenths. We can simplify this further by dividing the numerator and denominator by two to get three and two fifths. Three point four is the same as three and two fifths! While Tank enters the last code to unlock his shell phone let's review! Remember, to convert decimals greater than one to fractions, first, write the decimal on the place value chart. Next, convert any fractions that need adding, so that they have the same denominator. Finally, find the sum and simplify if needed. "And then my Mum was like, 'don't forget your turtleneck!', can you believe that!?" "Oh no, here we go."
Decimals Greater than 1 exercise
-
What does a decimal represent?
HintsDecimals can be greater than one.
Decimals and fractions represent the same number, but in different forms.
SolutionA decimal represents a whole number and a fractional part of a whole number. We use decimals when counting money and measuring objects, so it is important to understand what they represent.
-
What are the steps to convert a decimal greater than 1 to a fraction?
HintsIn this example, the decimals have been converted to improper fractions.
- 1.1 is equal to $\frac{11}{10}$.
- 1.11 is equal to $\frac{111}{100}$.
Here, the fractions have been converted to all have the same denominator of 100.
SolutionThe steps to converting a decimal greater than one to a fraction are as follows:
- Write the decimal in the place value chart.
- Write each place value as a fraction.
- Convert the fractions so they have a the same denominator.
- Find the sum and simplify if needed.
-
Which equation best represents the decimal 4.23?
HintsRemember to find the greatest denominator and convert the other fractions to have the same denominator.
This example shows you how to write each place as a fraction before converting the denominators.
Convert all fractions to the greatest denominator. In this example, the greatest denominator is 100.
SolutionThe correct answer is $\frac{400}{100}$ + $\frac{20}{100}$ + $\frac{3}{100}$ = $\frac{423}{100}$. This simplifies to 4 $\frac{23}{100}$
As you can see in the picture, all the fractions need to have a denominator of 100 because it is the greatest. You convert each fraction to have a denominator of 100 by multiplying them by a multiple of ten. Once you do that, you can add the numerator of each fraction together to get your answer.
-
Match the decimal to the fraction.
HintsYou could convert the improper fractions in to mixed numbers first to help you, for example, $\frac{124}{100}$ = 1 $\frac{24}{100}$. This can then be written onto a place value chart.
In the example, you can see that the decimal has been expanded into the chart by place value. We then use this chart to create fractions.
Here is an example of how an improper fraction has been converted into a mixed number and a decimal.
SolutionThe matches are:
- 2.67 and $\frac{267}{100}$
- 5.6 and $\frac{56}{10}$
- 7.8 and $\frac{78}{10}$
- 4.25 and $\frac{425}{100}$
-
Expand and convert the decimal 2.97.
HintsWhen looking at a number, do we read it left to right or right to left?
The tenths column means the fraction is out of 10 and the hundredths column means the fraction is out of 100.
In the decimal 6.5, the 5 is in the tenths place because it represents $\frac{5}{10}$ .
SolutionThe position of the number tells its value, e.g. the 2 represents two ones, the 9 is in the tenths place so represents nine tenths and the 7 is in the hundredths place so represents seven hundredths.
You then have to convert the decimal to fractions which looks like this: 2 $\frac{9}{10}$ $\frac{7}{100}$
-
Match the place value chart to the equations.
HintsWrite the decimal onto a place value chart to find how many ones, tenths and hundredths it is made up of.
When the fractions are added, convert an improper fraction to a mixed number, e.g. $\frac{54}{10} = 5\frac{4}{10}$.
SolutionWe use place value to expand decimals and think about the digits and their values.
Let's take a closer look at the first decimal. 6.7 is $\frac{60}{10}$ + $\frac{7}{10}$ which equals $\frac{67}{10}$ This is equivalent to 6 wholes and 7 tenths. This same concept applies to the rest of the problems.
- 8.43 is $\frac{800}{100}$ + $\frac{40}{100}$ + $\frac{3}{100}$
- 1.25 is $\frac{100}{100}$ + $\frac{20}{100}$ + $\frac{5}{100}$
- 3. 6 is $\frac{30}{10}$ + $\frac{6}{10}$
- 4.5 is $4\frac{5}{10}$
- 4.05 is $4\frac{5}{100}$
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?




















