Prime Numbers and Composite Numbers
Basics on the topic Prime Numbers and Composite Numbers
Prime Numbers and Composite Numbers
What are prime numbers and what are composite numbers? Let’s learn about prime and composite numbers in this text.
All numbers, starting with one, that we use for counting are called natural numbers. Natural numbers can be divided into two groups based on the number of factors they have.
These natural numbers are either prime or composite. So, what do prime and composite mean? The prime and composite definition is the following:
| Term | Definition |
|---|---|
| prime number | Any number that has only two factors – the number 1 and itself. |
| composite number | Any number with more than two factors. |
Determining Prime and Composite Numbers
How can you determine if a number is prime or composite? We can use our number sense, or knowledge of numbers, to determine if a number is prime or composite. To prove whether a number is prime or composite, think of the sets of factors that can be multiplied together to make the number. If there are only the factors of 1 and the number, it is a prime number. If there is more than one set of factor pairs, then the number is composite.
Prime and Composite Numbers – Examples
Let’s have a look at some examples of natural numbers:
The first number is 61. The factors are 1 and 61, so we can define 61 as a prime number.
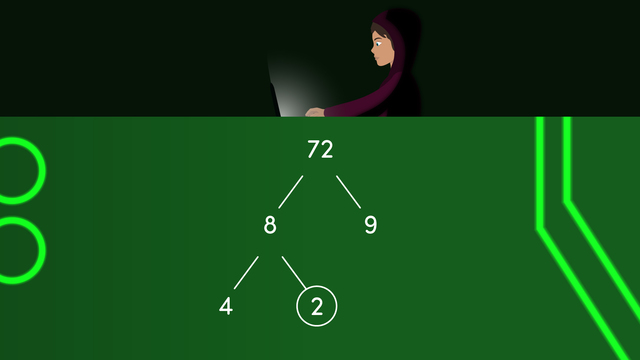
The second number is 50. Since 50 has more than two factors, it is a composite number.
The number is 1 is a special case. The factors are just 1 it is neither a prime nor a composite number.
Frequently Asked Questions about Prime and Composite Numbers
What are some questions about prime and composite numbers between 1-100? Let’s have a look:
Prime and Composite Numbers – Summary
Following the prime and composite video, there is additional practise on how to find prime and composite numbers. There are interactive exercises, activities and worksheets to enhance your understanding of how to do prime and composite numbers.
Transcript Prime Numbers and Composite Numbers
Skylar and Henry are returning from the farmer’s market with some new seeds. They were tired of always planting the same old things and wanted something that would really make their garden SING. As they got ready to plant, Skylar remembered what the merchant had told them. In order for your garden to really perform, you must plant these seeds in harmony. Prime number seeds stay together on one side and composite number seeds stay on the other. To work out which seeds should be planted together, we will need to help Sklyar and Henry determine ” Prime and Composite Numbers.” All numbers, starting with one, that we use for counting are called NATURAL NUMBERS. Natural numbers can be divided into two groups based on the number of factors they have. Prime numbers are the first group of natural numbers. A prime number is any number that has ONLY TWO factors: the number one and itself. "The other type of natural numbers are called composite numbers." A composite number is any number that has more than two factors. We can use our number sense, or knowledge of numbers, to determine if a number is prime or composite. Let’s look at the bags of seeds Skylar and Henry bought. The first bag contains seven seeds. Using number sense, how many ways can we evenly group these seeds in the garden? We can plant these seeds in one row of seven. Are there any other numbers we can multiply to get seven? No, since there are only two factors, one and seven, that make seven. Would we say seven is a prime or composite number?
The next bag has nine seeds inside. What is the first set of factors that we know make nine? We know that one times nine equals nine, so one and nine are factors. Are there any other numbers that group nine evenly? We can group nine into three rows of three, so three is a factor of nine. The factors of nine are one, three, and nine. Is nine a prime or composite number? Nine has three factors, so we say it is a COMPOSITE number. This bag is filled with fifty seeds. How can we determine if this number is prime or composite? We can see if there are more than two factors that make fifty. A number can always be made with one and itself, so we know that we can group by one times fifty. What else do we know about fifty that can help determine if it has more factors? "Fifty ends in a zero, so we know that it can be grouped by fives." Five times what would make fifty? Five times ten. Since fifty has more than two factors, fifty is a composite number. Fifty has more factors than what we found. Can you list all the factors of fifty? Write all the factors of fifty below in the comment section.
One last bag of seeds. This one has sixty-one seeds inside. Start with what we know. We know all natural numbers can be made by the factors of one and itself. Can we group sixty-one evenly in another way? No, if we try to group sixty-one by any other factor, there will always be a remainder. Is sixty-one, a prime or composite number? Sixty-one is a prime number. Skylar notices one seed stuck to her tail. She wondered where they were supposed to plant this one. The only way to make one is by multiplying one by itself, but that’s not two factors, so it CAN'T be prime. And since there aren’t any other factors, it CAN'T be composite either. One is a special natural number because it is the only number that is neither prime nor composite. Skylar took this special seed and planted it in a pot! Remember, natural numbers are all counting numbers starting with one. They can be prime or composite. Prime numbers only have TWO factors, one and itself. "Composite numbers have MORE THAN two factors." One is a special number because it's NEITHER prime nor composite. OH! Can you hear that? What is that sound?
Prime Numbers and Composite Numbers exercise
-
Prime or composite?
HintsRemember that a prime number has only two factors, one and itself. Factors are pairs of numbers that multiply together to get the target number. For example, factors of 8 are: 1 and 8, 2 and 4.
In a 2 digit number, look at the ones digit; if it is: 2, 4, 6, 8, 0, what does this tell you about the number?
Solution13 is a prime number. Its factors are 1 and 13.
23 is a prime number. Its factors are 1 and 23.
5 is a prime number. Its factors are 1 and 5.
17 is a prime number. Its factors are 1 and 17.
22 is a composite number. Its factors are: 1, 2, 11, 22.
35 is a composite number. Its factors are: 1, 5, 7, 35.
9 is a composite number. Its factors are: 1, 3, 9.
60 is a composite number. Its factors are: 1, 2, 4, 5, 6, 10, 12, 15, 20, 30, 60.
-
Find the factors.
HintsFactors come in pairs, so try to find your factors as pairs here. For example, a pair of factors for 20 would be 2 and 10 because 2 x 10= 20.
Remember, the seeds need to be arranged in even rows without any being left on the end.
SolutionThere are lots of ways that the seeds could be arranged. The factor pairs could be:
1 x 24
2 x 12
3 x 8
4 x 6
-
Decide whether each number is composite or prime.
HintsRemember that prime numbers have only two factors, one and itself.
To check whether a number has more than two factors, check whether it is divisible by numbers other than one and itself.
Solution- The Prime Numbers are: 2, 11, 13, 23. (2 is the only even prime number).
- The Composite Numbers are: 14, 27, 36, 49.
- Factors of the composite numbers:
- 14 = 1 x 14, 2 x 7
- 27 = 1 x 27, 3 x 9
- 36 = 1 x 36, 2 x 18, 3 x 12, 4 x 9, 6 x 6
- 49 = 1 x 49, 7 x 7
-
How many factors do I have?
HintsAre there any prime numbers? Remember that all prime numbers have only two factors.
To find all the factors that a number has, find all the pairs of numbers that multiply together to get that number.
Solution- 16 has 5 factors. (1, 2, 4, 8, 16).
- 20 has 6 factors. (1, 2, 4, 5, 10, 20).
- 14 has 4 factors. (1, 2, 7, 14).
- 7 has 2 factors. (1, 7).
-
How are prime and composite numbers defined?
HintsHere is an example of a prime number. How many factors does it have?
Some examples of composite numbers are: 12, 16, 20.
SolutionA prime number has two factors, one and itself.
A composite number has more than two factors.
-
Number detective.
HintsUse the clues you have to write down all the possibilities, then narrow these down by checking the number of factors.
Remember that prime numbers have only two factors and composite numbers have more than two factors.
Remember that all even numbers end in 2, 4, 6, 8, 0, and all odd numbers end in 1, 3, 5, 7, 9.
Solution- Number 1 = 4
- Number 2 = 2
- Number 3 = 15
- Number 4 = 16
Number 1. First find the even numbers less than 10. These are 2, 4, 6 and 8. 2 has two factors, 4 has three factors, 6 has four factors, and 8 has four factors. So the answer is 4.
Number 2. There is only one even prime number which is 2, as it only has 2 factors.
Number 3. The odd numbers between 10 and 20 are: 11, 13, 15, 17 and 19. The only composite number is 15; all the others are prime. So the answer is 15.
Number 4. The even numbers between 10 and 20 are: 12, 14, 16 and 18. 12 has 6 factors, 14 has 4 factors, 16 has 5 factors, and 18 has 6 factors. Since 16 is the only one with an odd number of factors, this is our answer.


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?















1 2 5 10 25 50
1 , 2 , 5 , 10 , 25 and 50!