Finding Missing Angles
Basics on the topic Finding Missing Angles
Adding and Subtracting Angles
Did you know that you can add and subtract angles? Adding and subtracting angles happens, when an angle gets smaller or larger. If an angle gets larger, we speak of additive angles. Additive angles are made from adjacent angles. Additive means we can use addition or subtraction to solve for unknown angle measurements.
Adjacent Angles – Definition
What are adjacent angles?
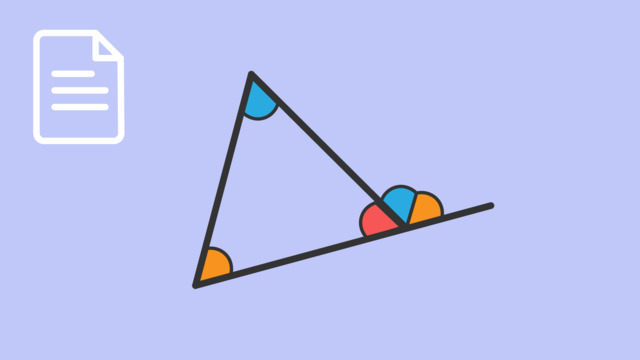
Adjacent angles are two angles that are next to each other but do not overlap. They share the same vertex and one side. Adjacent angles have smaller angles and also a larger one created when they are combined.
Adding Angles – Example
Finding the missing angle can be done by adding or subtracting adjacent angels. When Nico and Nia take off, the angles they make share the same vertex and one side. We know that Nia’s flight path makes a twenty degree angle and Nico’s is twenty five degrees higher, so what is Nico’s total angle?
We can use the information we know to find Nico’s angle. When adding angles, we can add the parts to find the whole. The first part is Nia’s angle, twenty degrees. The second part is the difference between their angles, twenty five degrees.
| part | + part | = whole |
|---|---|---|
| 20° | + 25° | = 45° |
Therefore, Nico’s flight made a forty five degree angle.
Subtracting Angles – Example
This time, Nico and Nia took off in different directions. We are given the measurement of the widest angle, as well as the angle Nico took off at. We need to find the difference between Nico and Nia’s angles.
This time, we know the whole and one part but need to find the other part. We will subtract the part we know from the whole.
| part | + part | = whole |
|---|---|---|
| 20° | + 25° | = 45° |
Therefore, the difference between their angles is one hundred and ten degrees.
Adding and Subtracting Angles – Summary
To continue learning, have a look at our finding missing angles worksheet with questions and answers training adding and subtracting angles. You can also have a go at our interactive exercises and further activities.
Transcript Finding Missing Angles
Wow! Check out Nico and Nia's new hang gliders! Each one of them thinks they can make it go higher so they decide to have a FRIENDLY competition! As their gliders lift off the ground, we can see that their flight patterns have created several angles. Today we will learn how we can use our addition and subtraction skills to find missing angles. "Finding Missing Angles" Nico and Nia's flights have created ANGLES. Let's look at the angles and see the line and the vertex they share. Their angles share the SAME VERTEX and ONE SIDE.
Let’s measure the angles made by Nico and Nia's flights. Nia’s flight made the first angle. We know that it measures twenty degrees. And Nico flew twenty-five degrees HIGHER. How can we solve to find the TOTAL angle of Nico’s flight? We know the parts, so we can ADD to find the whole angle. What is the sum of twenty and twenty-five? "Zero plus five is five, and two plus two makes four. " Forty-five! Nico’s flight was at a forty-five degree angle! NICO WON! "No, no, no!" "It's the BEST OUT OF THREE. That's how we decide the winner!" For the NEXT round, they decide to take off from a hill to give themselves more height. "What observations can you make about the angles made by where they took off and the directions they went in?" We can see the widest angle is made from the tree to the bottom of the hill, and Nia and Nico have now created a total of THREE angles inside. Nico flew at a sixty-six-degree angle off the ground. Nia's take off was seventeen degrees higher than Nico's, AND her flight path was twenty-six degrees from the tree. What do we need to do to find the angle measurement made by the tree to the ground? We need to ADD the three angles to find the sum. What is the total of sixty-six, plus seventeen, plus twenty-six? In the ones, six plus seven is thirteen. What is six more? Nineteen. "In the tens, add six plus one plus two to make nine, and now add one more." The total angle is one hundred and nine degrees. Since Nia flew higher in round two, it's time to get SERIOUS for the tiebreaker!
BLAST OFF!
Nico and Nia took off in opposite directions and have created new angles with the ground. What do you observe about these angles? Here we are given the total of the widest angle, and the measurement of Nia's angle. What do you think we need to do to find the MISSING angle, which is the DIFFERENCE between Nico and Nia’s flight? In this problem, we will need to SUBTRACT the KNOWN angle from the WHOLE to find the missing angle. This means whole minus part equals part. We set up the problem, one hundred and forty MINUS thirty. Start subtracting with the ones. There are zero ones. Four minus three equals one. We still have one in the hundreds because we didn’t have any to take away. The unknown angle measures one hundred and ten degrees. "Remember, we can use known angle measurements to find the unknown parts." In a group of angles that are joined together by one vertex, we can add the smaller angles to find the sum of the degrees of the widest angle. Or sometimes, we know the combined angle measurement and we need to find a missing part. We solve these by taking the angle degrees we do know and subtracting that number from the whole. "WOAH! WOAH! WOAH!" "NICO! HELP!"
"NIA!! HANG ON!" "I'M ON MY WAY!"
“Thank you, Nico!” “Shall we do it again?”
Finding Missing Angles exercise
-
Testing the gliders.
HintsRead the text to find the angles of Nico and Nia and where they can be marked on the image.
Find the largest angle by adding the two smaller angles together.
SolutionNia's glider made an angle of 40°, this is shown in green. Nico's glider made an angle of a further 38°, this is shown in pink. When we add this on to Nia's angle: 40° + 38° = 78°. This is shown in orange.
-
What is the angle of Nico's flight?
HintsAs Nico flew 20° higher than Nia, we need to add 20° onto Nia's angle to find the angle of Nico's flight.
What is 20 + 35?
Solution- To find the angle that Nico's glider flew from the ground, we need to add 20° to Nia's angle, as we know that Nico flew 20° higher than Nia.
- Nia flew 35° and Nico flew 20° higher.
- 35° + 20° = 55°.
- So Nico's glider flew 55° from the ground.
-
Find the missing angle.
HintsTo find a missing angle when we know the total of 2 adjacent angles, take the known angle from the total.
What is the calculation that needs to be completed?
Solution- Nico and Nia both make angles with their gliders that total 75°.
- As Nia's angle is 43°, to find Nico's angle we must subtract 43° from 75°.
- This will give us the missing angle.
- When we take 43° from 75° we get 32°, so this is the angle made by Nico.
-
Missing angles.
HintsWhere two adjacent angles have been given, the total of these can be found by adding them together.
If one adjacent angle has been given, subtract this from the total to find the missing angle.
Look carefully where the question mark is to find the correct missing angle.
Remember that we can recognise a right angle as 90° because it is marked by a small square like this,
SolutionThe solution image shows how the missing angle can be found for each question.
-
Which image shows adjacent angles?
HintsAdjacent angles share one straight line and a vertex.
Adjacent angles are next to each other. Remember, we are just looking at the angles marked in pink and green.
Solution- The angles shown in a) are adjacent because they share a vertex and one straight line. This is the CORRECT answer.
- The angles shown in b) do not share a vertex or straight line.
- The angles shown in c) share a vertex but do not share a straight line.
- The angles shown in d) share a vertex but do not share a straight line.
-
Angles in a circle.
HintsLook at the right angles marked in the circle. Can this help you to find the missing angles?
Remember that there are 90° in a quarter turn or a right angle, and 180° in a half turn or on a straight line.
Solution- To find angle a: We can see that there is a little square that means a right angle, which means that the angle is 90°.
- To find angle b: The top right quarter of the circle is shown by a right angle, this is then split into two adjacent angles. One of these is given as 37°. To find the missing angle, we need to subtract 37° from 90° to get 53°.
- To find angle c: There are two right angle symbols on the top half of the circle, so we know that the line going horizontally across the circle is a straight line, and angles on a straight line must add up to 180°. As one of these adjacent angles is given here as 132°, we then subtract 132° from 180° to get 48°.


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?